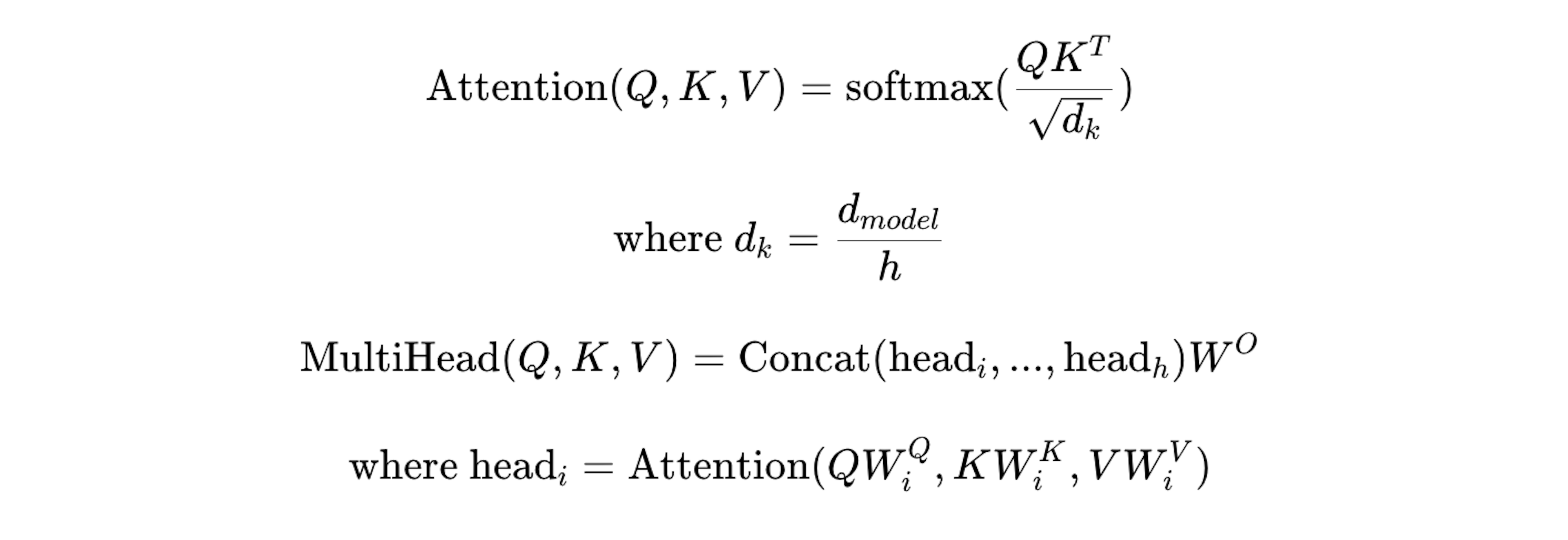自然语言处理-Transformer模型

第一章 Transformer介绍

第一节 引言

Transformer模型在2017年的论文《Attention is All You Need》中被提出，它在自然语言处理（NLP）领域引发了突破性的变革。该论文通过对英语翻译成德语和英语翻译成法语的机器翻译任务进行性能评估，发现Transformer在精度（Bleu分数）和训练成本方面都超过了之前最高精度的基于RNN的机器翻译模型。

此后，基于Transformer的各种模型被提出，例如BERT、XLNet、GPT-3等，这些模型在近年来被认为是最先进（State-of-the-Art, SoTA）的模型。

Transformer的名称意为变形金刚、变压器、转换，象征着其在各种任务中的强大适应能力。

在神经机器翻译中，Transformer模型使用了将一种时间序列数据转换成另一种时间序列数据的Encoder-Decoder（seq2seq）结构，这一点与基于RNN（如LSTM、GRU）的模型相同。然而，Transformer的最大特点是在Encoder和Decoder中都不存在像RNN那样的递归计算层，取而代之的是注意力机制。

Transformer不仅在自然语言处理中表现优异，在其他领域也被广泛使用，展现出很高的通用性。主要的深度学习框架如PyTorch和TensorFlow都已经有官方的实现，因此在研究和应用中使用这些框架已经成为一种普遍的做法。

为了理解Transformer的底层结构和原理，本文将介绍构成Transformer模型的各个层的理论背景，并通过PyTorch实现进行讲解和演示。

第二节 简化代码实现Pytorch版本

import torch
import torch.nn as nn

# 定义Transformer模型
class Transformer(nn.Module):
    def __init__(self, input_dim, output_dim, hidden_dim, num_layers):
        super(Transformer, self).__init__()

        # 编码器和解码器的初始化
        self.encoder = nn.TransformerEncoderLayer(input_dim, hidden_dim, num_layers)
        self.decoder = nn.TransformerDecoderLayer(output_dim, hidden_dim, num_layers)

    def forward(self, src, tgt):
        # 编码器的前向传播
        enc_output = self.encoder(src)

        # 解码器的前向传播
        dec_output = self.decoder(tgt, enc_output)

        return dec_output

# 创建Transformer模型实例
input_dim = 100
output_dim = 200
hidden_dim = 256
num_layers = 4
model = Transformer(input_dim, output_dim, hidden_dim, num_layers)

# 定义输入和目标数据
src = torch.randn(50, input_dim)
tgt = torch.randn(60, output_dim)

# 进行前向传播
output = model(src, tgt)

第二章 Transformer结构

第一节 Transformer总体结构

让我们来看一下《Attention is all you need》中所配的Transformer结构图。Transformer 模型依赖于两个独立、较小的模型：编码器和解码器。

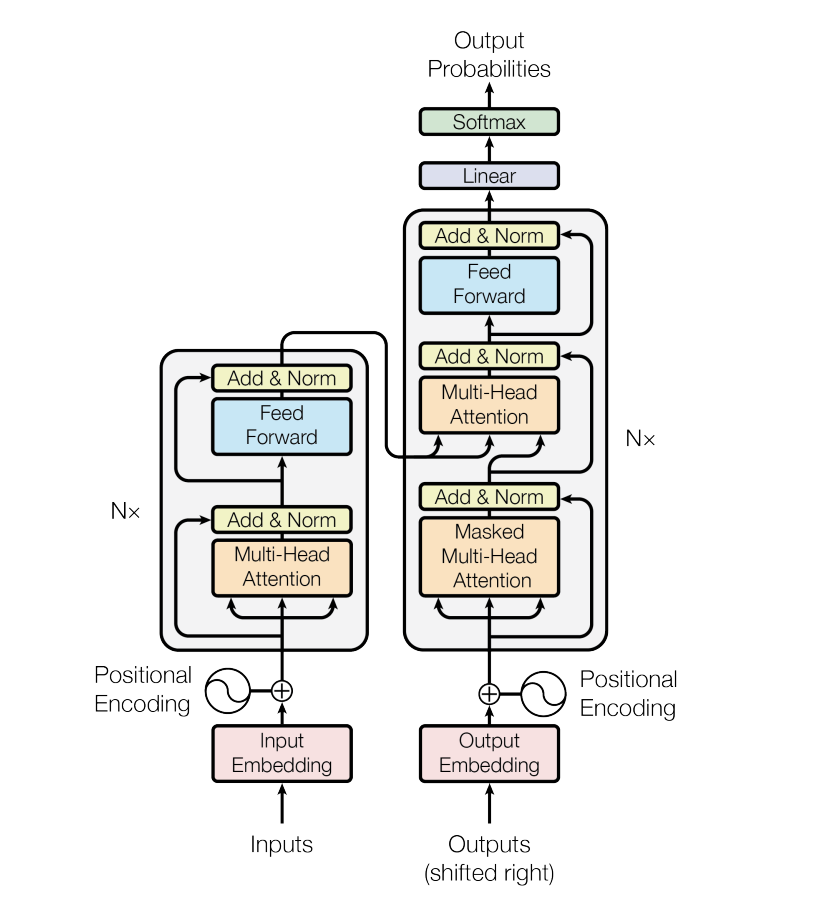
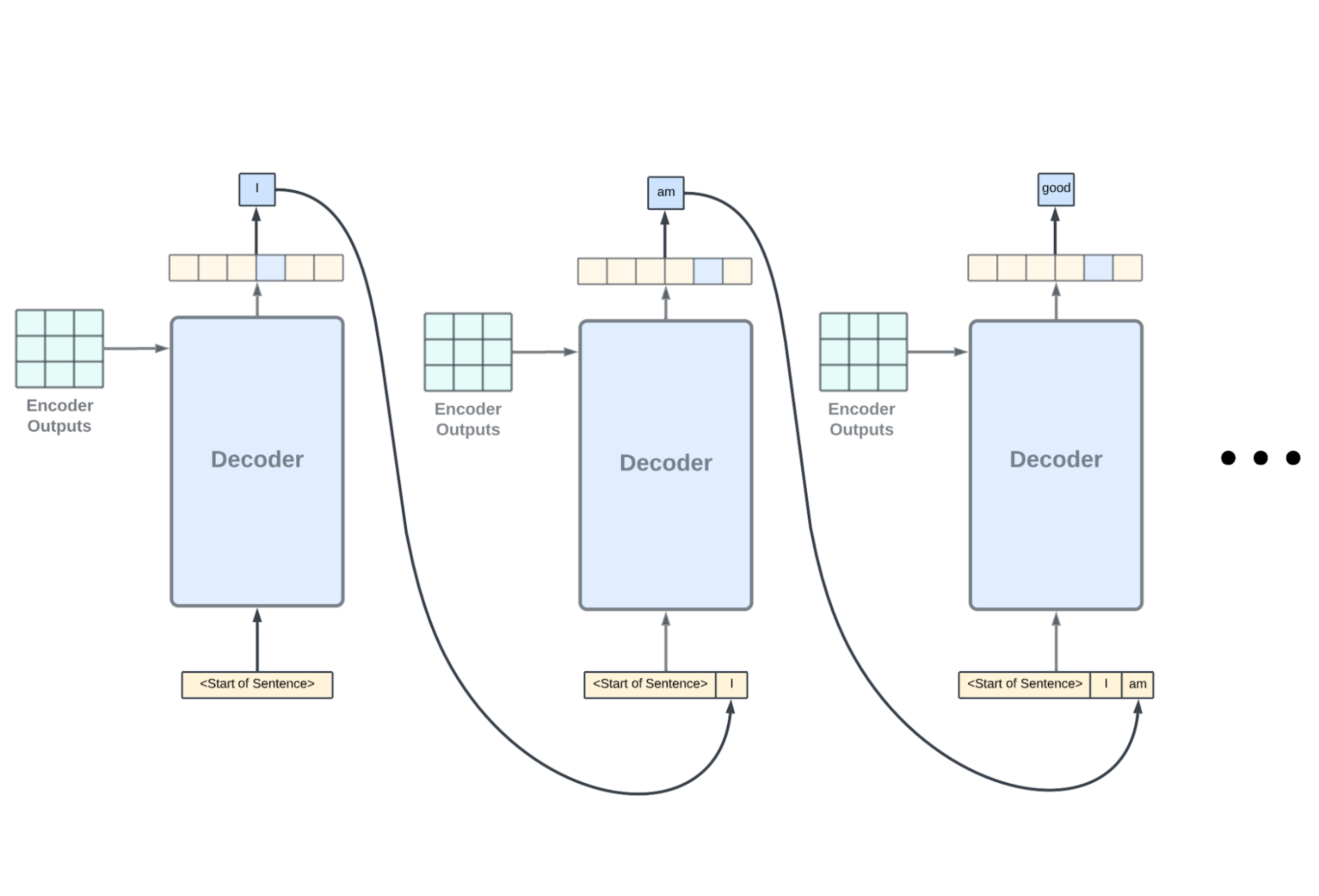
编码器接收输入，而解码器输出预测。

在编码器-解码器架构出现之前，序列问题的预测完全基于对输入序列的累积记忆，这些记忆被“压缩”为一个隐藏状态的表示。尽管 LSTM 和 GRU 等架构试图改善长程依赖问题，但它们并没有完全解决 RNN 的根本问题，即无法完全通过预测来承载长序列的信息。

在编码器-解码器架构中，编码器接收整个输入序列。它将其转换为矢量化表示，其中包含每个时间步骤中输入序列的累积记忆。然后，输入序列的整个矢量化表示被输入到解码器中，解码器“解码”编码器收集的信息并尝试做出有效预测。

第二节 编码器

2.2.1 编码器原理

Transformer像Seq2seq一样的形式，具有Encoder-Decoder结构。

编码器负责将输入序列转换为机器可读的表示，这个过程会捕获单词之间的相似性及其在序列中的相对位置。输入序列首先经过输入嵌入和位置编码层。这些操作是为了输入的单词转换为适合编码器层处理的形式。

编码器层（也就是上面灰色的部分）是编码器的核心，大部分“魔法”都发生在这里。

在原始论文中，建议将编码器层的N设置为6，也就是堆叠六次。编码器由一个多头注意力块组成，后面跟着一个前馈神经网络，该神经网络在两个输出后都有残差连接和层规范化。

多头注意力模块能够发现单词之间的复杂关系，并确定每个单词对输入序列含义的贡献。这使得编码器能够像人类一样理解语言。

在编码器层之后，前馈网络会进一步转换输入序列，为下一个编码器层做准备。编码过程完成后，编码器获得的累积知识（最后一个编码器层的输出）将传递给解码器，解码器会利用这些知识生成最终的输出序列。

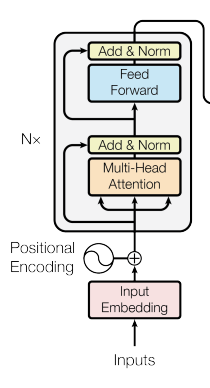
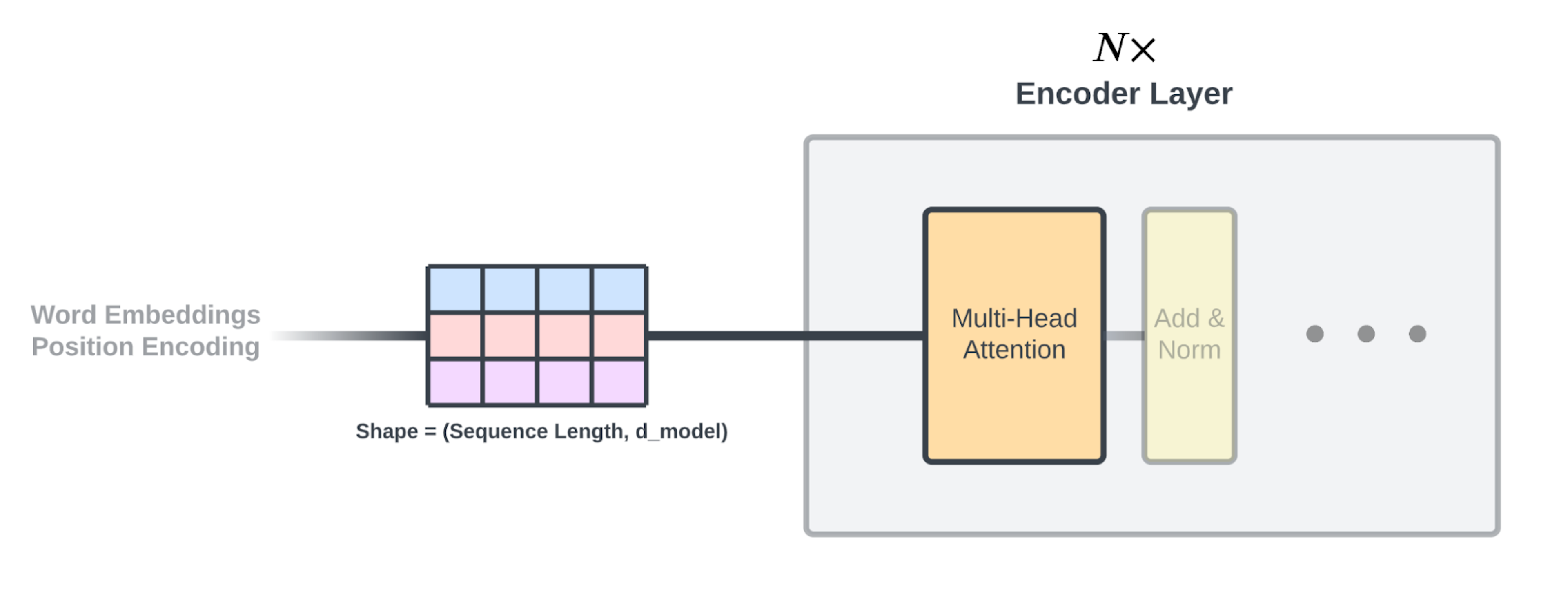
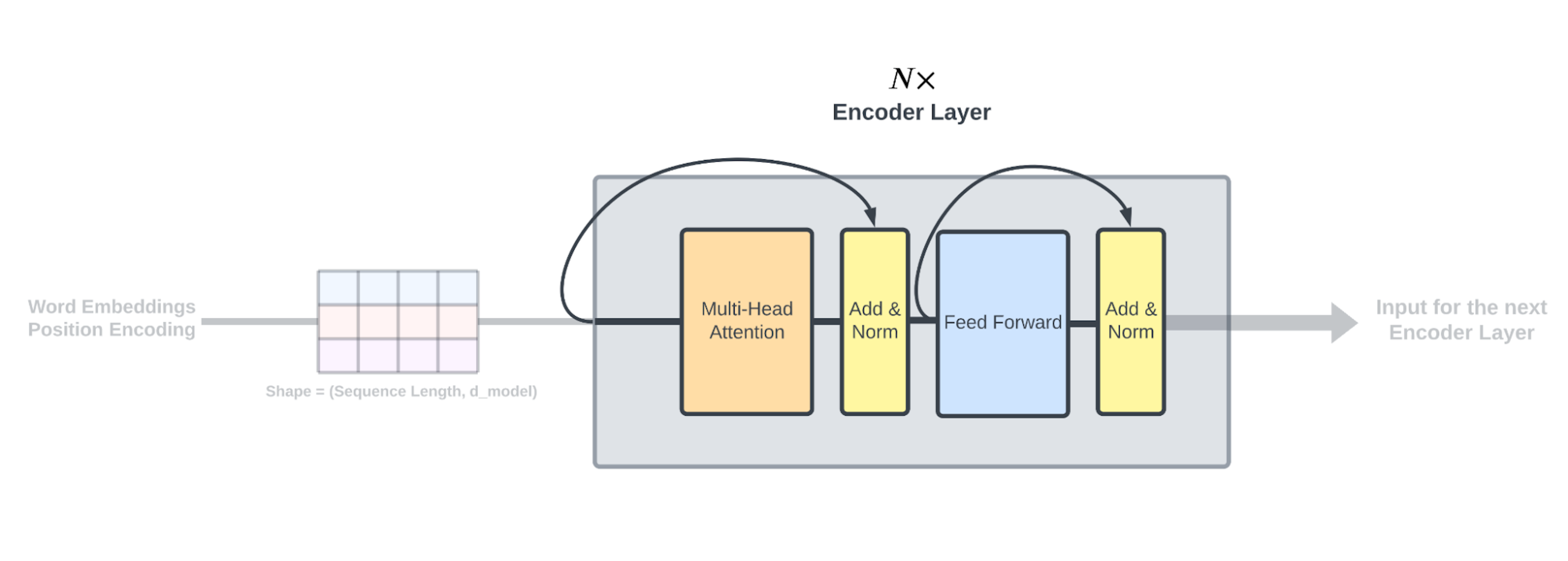
因此，TransformerEncoder由以下三个主要部分组成：

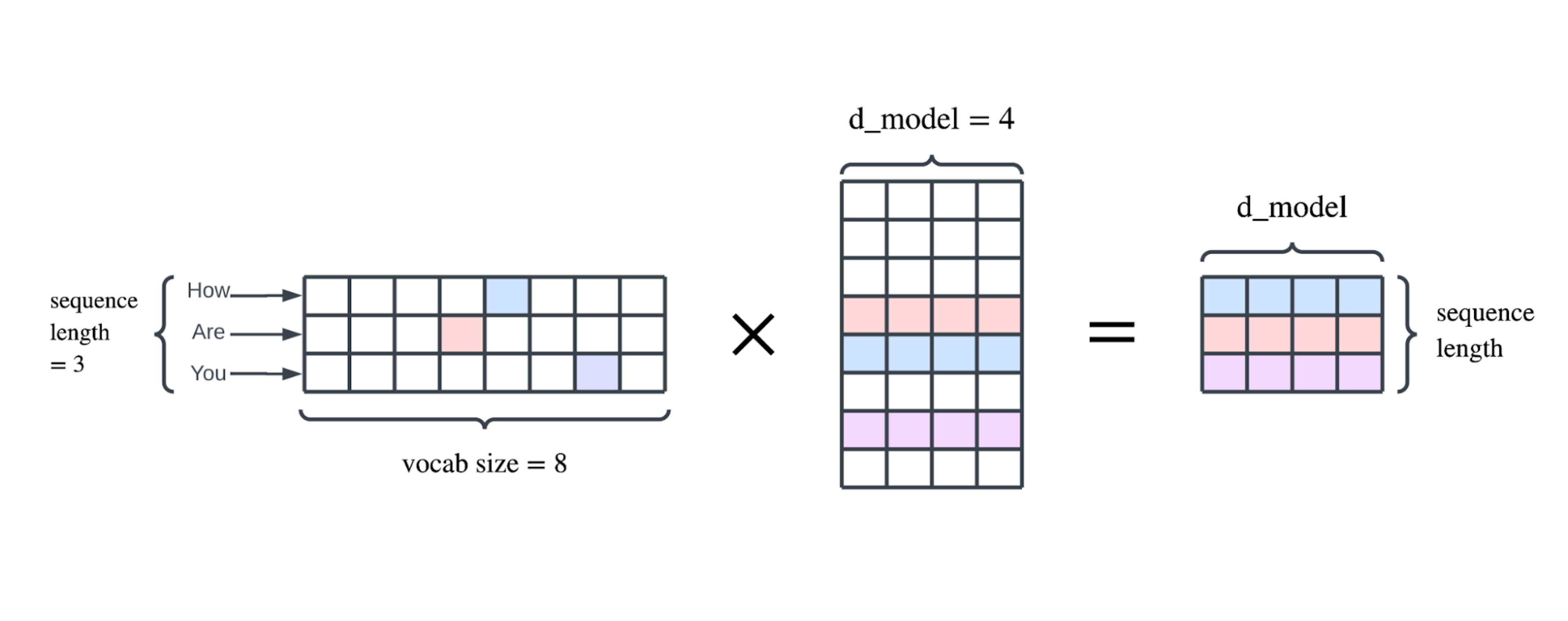
• Embedding层（将单词ID序列转换为单词的分布表示）
• Positional Encoding层
• 由任意N层堆叠的TransformerEncoderBlock层，包括Multihead Attention和FeedForward Network（每层都应用Add & Norm）

2.2.2 代码实现

import torch
from torch import nn
from torch.nn import LayerNorm

# 引入模块中的其他自定义类
from .Embedding import Embedding
from .FFN import FFN
from .MultiHeadAttention import MultiHeadAttention
from .PositionalEncoding import AddPositionalEncoding

class TransformerEncoderLayer(nn.Module):
    # Transformer编码器层的初始化方法
    def __init__(
        self,
        d_model: int,           # 模型的维度
        d_ff: int,              # _feed-forward网络的维度
        heads_num: int,         # 多头注意力中头的数量
        dropout_rate: float,    # dropout率
        layer_norm_eps: float,  # LayerNorm的epsilon值
    ) -> None:
        super().__init__()      # 调用基类的初始化方法

        # 初始化多头注意力层
        self.multi_head_attention = MultiHeadAttention(d_model, heads_num)

        # 初始化self-attention的dropout层
        self.dropout_self_attention = nn.Dropout(dropout_rate)

        # 初始化self-attention的LayerNorm
        self.layer_norm_self_attention = LayerNorm(d_model, eps=layer_norm_eps)

        # 初始化_feed-forward网络
        self.ffn = FFN(d_model, d_ff)

        # 初始化_ffn的dropout层
        self.dropout_ffn = nn.Dropout(dropout_rate)

        # 初始化_ffn的LayerNorm
        self.layer_norm_ffn = LayerNorm(d_model, eps=layer_norm_eps)

    # 前向传播方法
    def forward(self, x: torch.Tensor, mask: torch.Tensor = None) -> torch.Tensor:
        # 进行self-attention操作，并将结果加上原始输入x
        x = self.layer_norm_self_attention(self.__self_attention_block(x, mask) + x)

        # 进行_feed-forward操作，并将结果加上self-attention的结果
        x = self.layer_norm_ffn(self.__feed_forward_block(x) + x)

        return x

    # 自定义的self-attention块
    def __self_attention_block(self, x: torch.Tensor, mask: torch.Tensor) -> torch.Tensor:
        # 多头注意力操作
        x = self.multi_head_attention(x, x, x, mask)

        # 对多头注意力的结果进行dropout操作
        return self.dropout_self_attention(x)

    # 自定义的_feed-forward块
    def __feed_forward_block(self, x: torch.Tensor) -> torch.Tensor:
        # 通过_feed-forward网络
        return self.dropout_ffn(self.ffn(x))

class TransformerEncoder(nn.Module):
    # Transformer编码器的初始化方法
    def __init__(
        self,
        vocab_size: int,        # 词汇表的大小
        max_len: int,           # 输入序列的最大长度
        pad_idx: int,           # padding的索引
        d_model: int,           # 模型的维度
        N: int,                 # 编码器层的数量
        d_ff: int,              # _feed-forward网络的维度
        heads_num: int,         # 多头注意力中头的数量
        dropout_rate: float,    # dropout率
        layer_norm_eps: float,  # LayerNorm的epsilon值
        device: torch.device = torch.device("cpu"),  # 指定设备，默认为CPU
    ) -> None:
        super().__init__()      # 调用基类的初始化方法

        # 初始化词嵌入层
        self.embedding = Embedding(vocab_size, d_model, pad_idx)

        # 初始化位置编码层
        self.positional_encoding = AddPositionalEncoding(d_model, max_len, device)

        # 初始化Transformer编码器层的列表
        encodelayerList = [TransformerEncoderLayer(d_model, d_ff, heads_num, dropout_rate, layer_norm_eps) for _ in range(N)] # 创建N层编码器层

        self.encoder_layers = nn.ModuleList(encodelayerList)

    # 编码器的前向传播方法
    def forward(self, x: torch.Tensor, mask: torch.Tensor = None) -> torch.Tensor:
        # 将输入x通过词嵌入层
        x = self.embedding(x)

        # 将位置编码加到词嵌入的结果上
        x = self.positional_encoding(x)

        # 遍历所有编码器层，并进行前向传播
        for encoder_layer in self.encoder_layers:
            x = encoder_layer(x, mask)

        return x

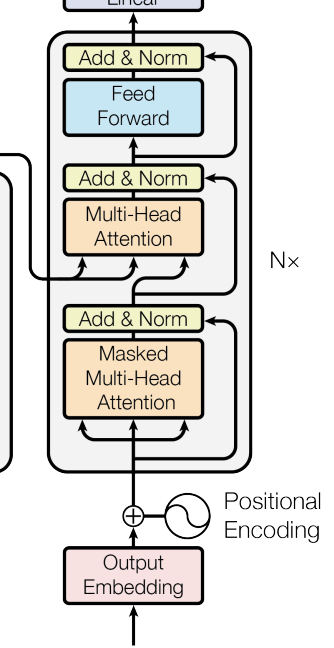
第三节 解码器

2.3.1 解码器原理

解码器接收编码器的输出，这是编码器已经理解好了的知识。

在第一个预测时间步，解码器设置“句子开头”标记，这有助于解码器理解输入的文本是一个新的句子。

解码器根据已有的预测知识进行分析，得出初步的见解。然后，解码器将这些初步的见解与编码器的输出相结合，进行更深入的处理和分析。最后，解码器输出下一个时间步骤的预测，即所选单词成为输出序列中下一个单词的概率。

Decoder与Encoder一样，由Embedding、Positional Encoding、Multihead Attention、FeedForward Network组成。

2.3.2 代码实现

import torch
from torch import nn
from torch.nn import LayerNorm

# 引入模块中的其他自定义类
from .Embedding import Embedding
from .FFN import FFN
from .MultiHeadAttention import MultiHeadAttention
from .PositionalEncoding import AddPositionalEncoding

class TransformerDecoderLayer(nn.Module):
    # Transformer解码器层的初始化方法
    def __init__(
        self,
        d_model: int,           # 模型的维度
        d_ff: int,              # 馈前网络（Feed-Forward Network）的维度
        heads_num: int,         # 多头注意力中头的数量
        dropout_rate: float,    # dropout率
        layer_norm_eps: float,  # LayerNorm的epsilon值
    ):
        super().__init__()      # 调用基类的初始化方法

        # 初始化目标自身的多头注意力层
        self.self_attention = MultiHeadAttention(d_model, heads_num)

        # 初始化目标自身注意力的dropout层
        self.dropout_self_attention = nn.Dropout(dropout_rate)

        # 初始化目标自身注意力的LayerNorm
        self.layer_norm_self_attention = LayerNorm(d_model, eps=layer_norm_eps)

        # 初始化源-目标的多头注意力层
        self.src_tgt_attention = MultiHeadAttention(d_model, heads_num)

        # 初始化源-目标注意力的dropout层
        self.dropout_src_tgt_attention = nn.Dropout(dropout_rate)

        # 初始化源-目标注意力的LayerNorm
        self.layer_norm_src_tgt_attention = LayerNorm(d_model, eps=layer_norm_eps)

        # 初始化馈前网络
        self.ffn = FFN(d_model, d_ff)

        # 初始化馈前网络的dropout层
        self.dropout_ffn = nn.Dropout(dropout_rate)

        # 初始化馈前网络的LayerNorm
        self.layer_norm_ffn = LayerNorm(d_model, eps=layer_norm_eps)

    # 解码器层的前向传播方法
    def forward(
        self,
        tgt: torch.Tensor,           # 解码器的输入
        src: torch.Tensor,           # 编码器的输出
        mask_src_tgt: torch.Tensor,  # 源-目标注意力的掩码
        mask_self: torch.Tensor,     # 目标自身注意力的掩码
    ) -> torch.Tensor:
        # 目标自身注意力操作
        tgt = self.layer_norm_self_attention(
            tgt + self.__self_attention_block(tgt, mask_self)
        )

        # 源-目标注意力操作
        x = self.layer_norm_src_tgt_attention(
            tgt + self.__src_tgt_attention_block(src, tgt, mask_src_tgt)
        )

        # 馈前网络操作
        x = self.layer_norm_ffn(x + self.__feed_forward_block(x))

        return x

    # 自定义的源-目标注意力块
    def __src_tgt_attention_block(
        self, src: torch.Tensor, tgt: torch.Tensor, mask: torch.Tensor
    ) -> torch.Tensor:
        # 源-目标注意力操作，使用编码器的输出作为键和值
        return self.dropout_src_tgt_attention(
            self.src_tgt_attention(tgt, src, src, mask)
        )

    # 自定义的目标自身注意力块
    def __self_attention_block(
        self, x: torch.Tensor, mask: torch.Tensor
    ) -> torch.Tensor:
        # 目标自身注意力操作
        return self.dropout_self_attention(self.self_attention(x, x, x, mask))

    # 自定义的馈前网络块
    def __feed_forward_block(self, x: torch.Tensor) -> torch.Tensor:
        # 馈前网络操作
        return self.dropout_ffn(self.ffn(x))

class TransformerDecoder(nn.Module):
    # Transformer解码器的初始化方法
    def __init__(
        self,
        tgt_vocab_size: int,    # 目标词汇表的大小
        max_len: int,           # 输入序列的最大长度
        pad_idx: int,           # 填充索引
        d_model: int,           # 模型的维度
        N: int,                 # 解码器层的数量
        d_ff: int,              # 馈前网络的维度
        heads_num: int,         # 多头注意力中头的数量
        dropout_rate: float,    # dropout率
        layer_norm_eps: float,  # LayerNorm的epsilon值
        device: torch.device = torch.device("cpu"),  # 指定设备，默认为CPU
    ) -> None:
        super().__init__()  # 调用基类的初始化方法

        # 初始化词嵌入层
        self.embedding = Embedding(tgt_vocab_size, d_model, pad_idx)

        # 初始化位置编码层
        self.positional_encoding = AddPositionalEncoding(d_model, max_len, device)

        # 初始化解码器层的列表
        decodeLayerList = [
                TransformerDecoderLayer(
                    d_model, d_ff, heads_num, dropout_rate, layer_norm_eps
                )
                for _ in range(N)  # 创建N层解码器层
            ]
        self.decoder_layers = nn.ModuleList(decodeLayerList)

    # 解码器的前向传播方法
    def forward(
        self,
        tgt: torch.Tensor,           # 解码器的输入
        src: torch.Tensor,           # 编码器的输出
        mask_src_tgt: torch.Tensor,  # 源-目标注意力的掩码
        mask_self: torch.Tensor,     # 目标自身注意力的掩码
    ) -> torch.Tensor:
        # 将解码器的输入tgt通过词嵌入层
        tgt = self.embedding(tgt)

        # 将位置编码加到词嵌入的结果上
        tgt = self.positional_encoding(tgt)

        # 遍历所有解码器层，并进行前向传播
        for decoder_layer in self.decoder_layers:
            tgt = decoder_layer(
                tgt,
                src,
                mask_src_tgt,
                mask_self,
            )
        return tgt

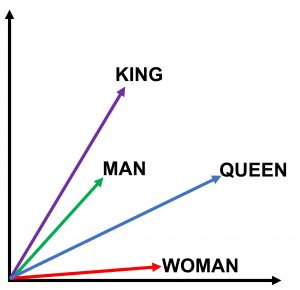
第四节 词嵌入

词嵌入目的是把给定输入序列转成机器可读的表示。常用独热编码，即每个单词由一个大且稀疏向量表示，仅在对应索引处有非零值，但此法低效且不优雅，会产生庞大向量，99%为零值，会因维数灾难影响模型性能，且能传达的信息极少。

词向量对稀疏独热编码向量进行从大型语料库中学到的进一步转换，产生考虑上下文的密集、相对低维单词表示。

如在“猫是棕色和毛茸茸的，而冰箱是一台毫无生气的银色机器”中，“猫”和“冰箱”词向量差异大，“棕色”和“银色”嵌入相似。通常用余弦相似度计算词向量距离。

如：king-man+women=queen，显示三者内在关系。

词嵌入可视为语言模型预训练技术，如果不用嵌入技术的话其实模型在训练时也可以学到每个单词上下文信息，只不过词嵌入可提前完成。

为有效生成密集词嵌入，可以选用各种方法和预训练算法，但 Transformer 用附加的词嵌入且从头训练，不用预初始化参数，让模型根据输入数据上下文和整体结构学习嵌入。词嵌入是 Transformer 首个组件，是通过 单词的独热编码输入 与 反向传播训练的权重矩阵相乘得到 词嵌入向量。

权重矩阵形状为（词汇量、嵌入维度），按原论文称嵌入维度为“$d_{model}$”，作者设其为 $512$。词向量可看成将独热编码向量映射到低维空间的查找表，通过 输入向量 × 权重矩阵 实现降维，能捕捉单词依赖关系和提供上下文信息。

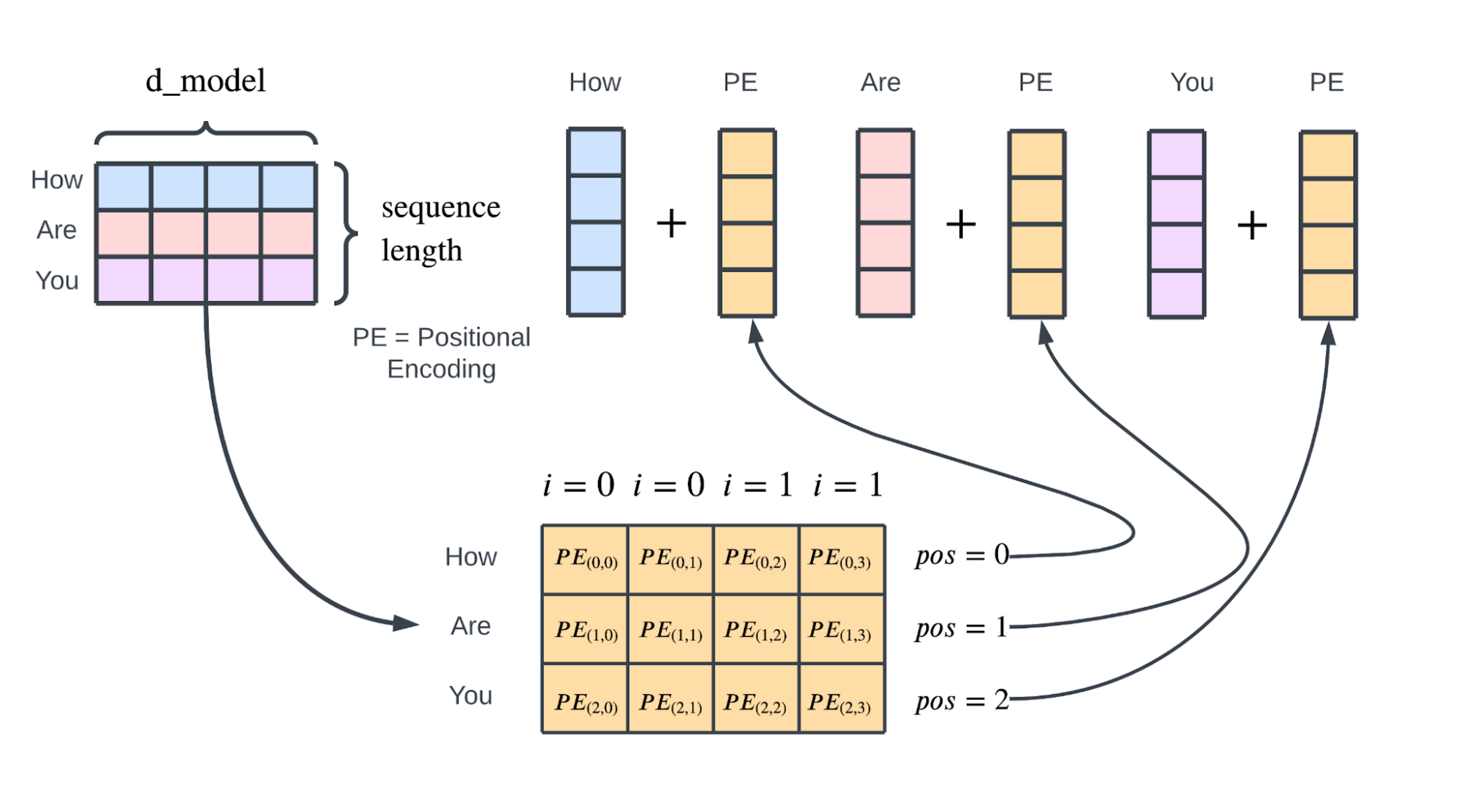
第五节 位置编码

2.5.1 位置编码原理

Positional Encoding Layer（位置编码层）主要负责赋予序列数据中每个元素其在数据内的位置信息。

Transformer 架构摒弃了基于循环的网络，转而依靠自注意力机制来处理输入序列。虽然这样做能加快训练速度并优化对长距离依赖关系的处理，但它本身存在一个问题，即无法提供有关输入句子的单词相对位置信息。

例如，“我去打篮球”和“篮球打我”这两个句子中，根据“篮球”的位置传达了完全不同的含义。尽管如此，在这两种情况下“篮球”的词嵌入是相同的。如果是基于循环的模型，由于其按顺序处理信息，所以每个单词的位置自然就有所暗示，但 Transformer 需要额外的信息来区分这些不同位置的“篮球”。

为了解决这个问题，采用了位置编码，即为每个词嵌入向量添加一个长度为 $d_{model}$ 的独特向量。该位置编码向量由单词在输入序列中的位置决定。这样一来，模型能够提取输入中单词的相对位置，并将此信息纳入其处理过程中。

位置编码的具体实现方式通过以下两条公式来确定单词的位置信息：
$$
PE(pos, 2i) = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)
$$

$$
PE(pos, 2i + 1) = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)
$$

在上面的等式中，“pos”表示单词在输入序列中的位置，而“i”表示每个值在词嵌入中的位置。这两个位置编码函数均被应用，为每个“i”值产生两个独特值。所以，要输出长度为 $d_{model}$ 的向量，“i”的值将在 0 到 $d_{model}-1$ 之间。

此外，位置编码具有一些独特的性质。它使得模型能够捕捉到不同位置之间的相对关系，增加了模型对序列结构的理解能力。并且，位置编码的引入是相对灵活的，可以根据具体需求和场景进行调整和优化。

正弦位置编码具有几个优点：

1. 原始论文中已经指出，Transformer 能够利用位置编码函数“推断出比训练期间遇到的序列长度更长的序列”。
2. 单词之间的相对位置可以推断出来，因为对于位置彼此接近的单词，它们的位置编码向量也会相似。

位置编码组件之后，其形状为（序列长度，$d_{model}$）的输出将被传递到由自注意力块和前馈神经网络组成的第一个编码器层。

请注意，解码器的输入序列也使用相同的预处理方案（词嵌入和位置编码），我们将在后面讨论。

2.5.2 具体计算例子

假设我们的句子是“我去打篮球”，并且我们使用的模型嵌入维度 $d_{model}$ 是 4（为了简单起见，实际模型通常是 512 或 1024 等）。

词语和其位置：

“我”：位置 0

“去”：位置 1

“打”：位置 2

“篮球”：位置 3

嵌入维度 $d_{model}$ 是 4，所以我们有 $i = 0, 1$

位置编码计算

位置 0 (“我”)：

• $i = 0$:

  • $PE(0, 0) = \sin\left(\frac{0}{10000^{\frac{0}{4}}}\right) = \sin(0) = 0$
  • $PE(0, 1) = \cos\left(\frac{0}{10000^{\frac{0}{4}}}\right) = \cos(0) = 1$

• $i = 1$:

  • $PE(0, 2) = \sin\left(\frac{0}{10000^{\frac{2}{4}}}\right) = \sin(0) = 0$
  • $PE(0, 3) = \cos\left(\frac{0}{10000^{\frac{2}{4}}}\right) = \cos(0) = 1$

结果：$[0, 1, 0, 1]$

位置 1 (“去”)

• $i = 0$:

  • $PE(1, 0) = \sin\left(\frac{1}{10000^{\frac{0}{4}}}\right) = \sin(1) \approx 0.8415$
  • $PE(1, 1) = \cos\left(\frac{1}{10000^{\frac{0}{4}}}\right) = \cos(1) \approx 0.5403$

• $i = 1$:

  • $PE(1, 2) = \sin\left(\frac{1}{10000^{\frac{2}{4}}}\right) = \sin(0.0001) \approx 0.0001$
  • $PE(1, 3) = \cos\left(\frac{1}{10000^{\frac{2}{4}}}\right) = \cos(0.0001) \approx 1.0000$

结果：$[0.8415, 0.5403, 0.0001, 1.0000]$

位置 2 (“打”)

• $i = 0$:

  • $PE(2, 0) = \sin\left(\frac{2}{10000^{\frac{0}{4}}}\right) = \sin(2) \approx 0.9093$
  • $PE(2, 1) = \cos\left(\frac{2}{10000^{\frac{0}{4}}}\right) = \cos(2) \approx -0.4161$

• $i = 1$:

  • $PE(2, 2) = \sin\left(\frac{2}{10000^{\frac{2}{4}}}\right) = \sin(0.0002) \approx 0.0002$
  • $PE(2, 3) = \cos\left(\frac{2}{10000^{\frac{2}{4}}}\right) = \cos(0.0002) \approx 0.9999$

结果：$[0.9093, -0.4161, 0.0002, 0.9999]$

位置 3 (“篮球”)

• $i = 0$:

  • $PE(3, 0) = \sin\left(\frac{3}{10000^{\frac{0}{4}}}\right) = \sin(3) \approx 0.1411$
  • $PE(3, 1) = \cos\left(\frac{3}{10000^{\frac{0}{4}}}\right) = \cos(3) \approx -0.9899$

• $i = 1$:

  • $PE(3, 2) = \sin\left(\frac{3}{10000^{\frac{2}{4}}}\right) = \sin(0.0003) \approx 0.0003$
  • $PE(3, 3) = \cos\left(\frac{3}{10000^{\frac{2}{4}}}\right) = \cos(0.0003) \approx 0.9999$

结果：$[0.1411, -0.9899, 0.0003, 0.9999]$

位置编码结果表格：

位置	单词	$PE(pos, 0)$	$PE(pos, 1)$	$PE(pos, 2)$	$PE(pos, 3)$
0	我	0.0000	1.0000	0.0000	1.0000
1	去	0.8415	0.5403	0.0001	1.0000
2	打	0.9093	-0.4161	0.0002	0.9999
3	篮球	0.1411	-0.9899	0.0003	0.9999

2.5.3 代码实现

import numpy as np
import torch
from torch import nn

class AddPositionalEncoding(nn.Module):
    # 初始化位置编码类，它是一个PyTorch模型模块
    def __init__(
        self, d_model: int, max_len: int, device: torch.device = torch.device("cpu")
    ) -> None:
        super().__init__()      # 调用基类的初始化方法
        self.d_model = d_model  # d_model是模型的维度
        self.max_len = max_len  # max_len是序列的最大长度

        # 初始化位置编码权重，并通过to函数移动到指定的设备（CPU或GPU）
        positional_encoding_weight: torch.Tensor = self._initialize_weight().to(device)

        # 注册positional_encoding_weight为模型的缓冲区，这样PyTorch会跟踪其梯度
        self.register_buffer("positional_encoding_weight", positional_encoding_weight)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        # forward方法，将位置编码添加到输入x上
        seq_len = x.size(1)  # 获取输入序列的长度

        # 返回添加了位置编码的输入序列，位置编码的前seq_len个元素与输入序列的每个元素相加
        return x + self.positional_encoding_weight[:seq_len, :].unsqueeze(0)

    def _get_positional_encoding(self, pos: int, i: int) -> float:
        # 私有方法，用于计算单个位置编码的值
        w = pos / (10000 ** (((2 * i) // 2) / self.d_model))  # 计算权重

        # 根据i的奇偶性返回正弦或余弦值，用于位置编码
        if i % 2 == 0:
            return np.sin(w)
        else:
            return np.cos(w)

    def _initialize_weight(self) -> torch.Tensor:
        # 私有方法，用于初始化位置编码权重
        positional_encoding_weight = [
            [self._get_positional_encoding(pos, i) for i in range(1, self.d_model + 1)]
            for pos in range(1, self.max_len + 1)
        ]
        # 将位置编码权重转换为张量并返回
        return torch.tensor(positional_encoding_weight).float()

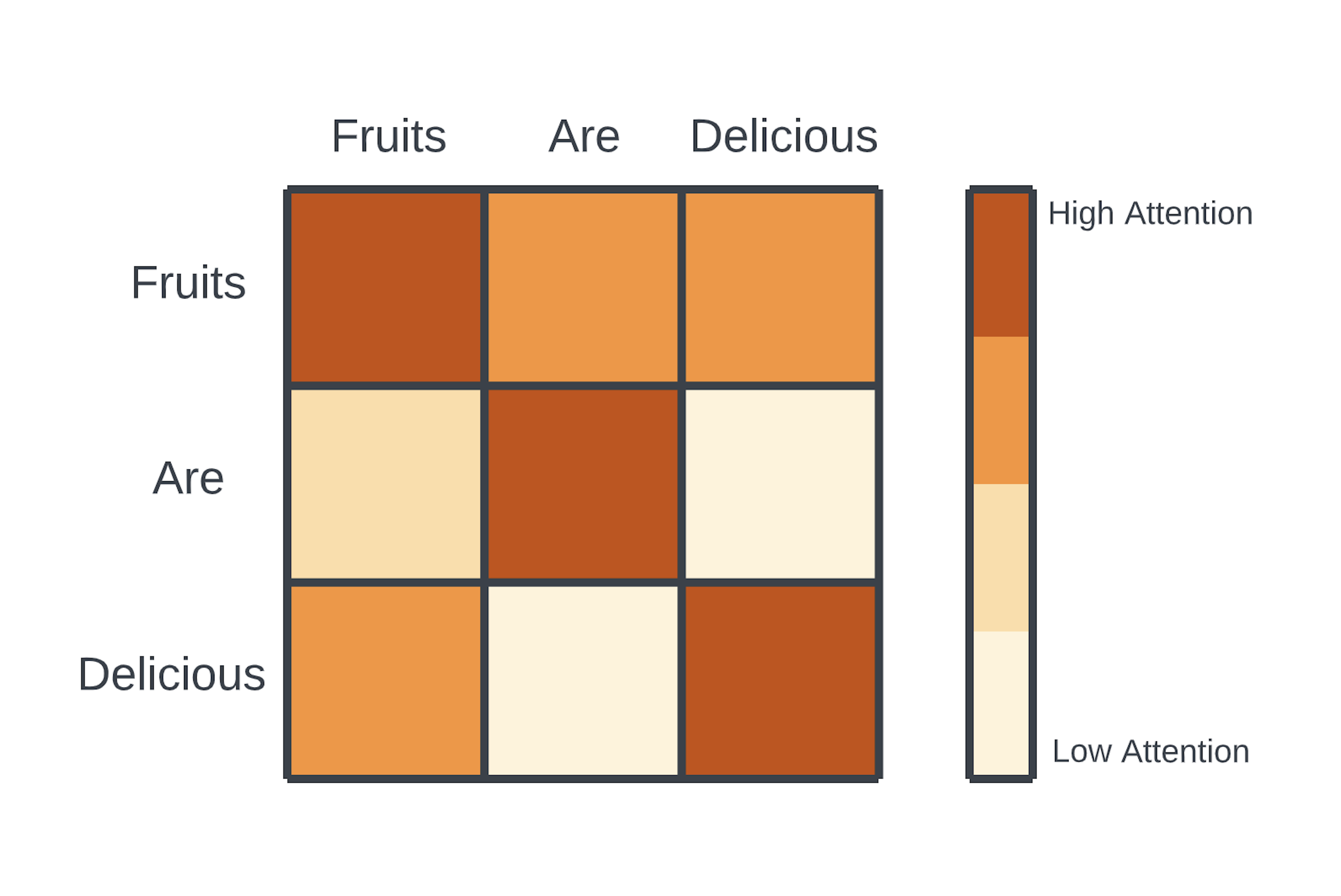
第六节 注意力机制

2.6.1 注意力机制原理

注意力或全局注意力通常是自然语言处理模型取得成功的最重要因素之一。

注意力的基本思想是：模型可以根据输入词与上下文的相关性，更关注某些输入词。换句话说，模型为每个输入词分配不同程度的“注意力”，越重要的词获得的关注越多。

比如在“我的狗有黑色、厚厚的皮毛，性格活泼。我还有一只棕色皮毛的猫。我的狗是什么品种的？”这个例子中，没有注意力模型会同等对待猫和狗信息，可能导致错误答案，而有注意力，训练后的语言模型会减少对“棕色皮毛”的关注，因其与问题无关，这种有选择关注重要单词的能力有助于提高自然语言处理模型性能。

自注意力机制类似于搜索引擎，查询就像您在搜索栏中输入的搜索查询，K键就像数据库中网站的标题，V值就像网站本身。当您输入搜索查询时，系统会将其与数据库中的键进行比较，并根据键与查询的相似程度对值进行排名。

理解自注意力如何分配 注意力值 一个有用方法：将输入序列的每个元素与序列中的其他元素进行比较来构建相关矩阵。

自注意力机制由三个部分组成：Q查询、K键和V值。每个单词的向量化表示被投影到三个较小的向量中，分别表示单词的Q查询、K键和V值。

2.6.2 注意力机制背后的数学原理

回想一下，位置编码的输出形状为 (序列长度，$d_{model}$)，其中 $d_{model}$ 可以解释为嵌入维度。此矩阵是编码器层的输入。对于第一个编码器层之后的编码器层，它们的输入将是前一个编码器层的输出。

输入矩阵通过三个单独的权重矩阵线性投影到三个较小的矩阵中，即 Q查询、K键 和 V值。

这些矩阵的形状为（序列长度：64），其中维度 64 是论文作者选择的任意值。

Q查询、K键和V值的权重矩阵分别称为 $W_Q$、$W_K$ 和 $W_V$。这些权重矩阵与整个模型一起通过反向传播进行训练。为矩阵维度选择的值 64 不会影响自注意力的计算。

在Transformer中，采用了一种称为ScaledDotProductAttention的方法来计算注意力权重，该方法通过计算 查询$Q$ 和输入 $K$ 的点积来计算 注意力权重。在下一节中，我们将详细看看这个方法。

第七节 缩放点积注意力(Scaled Dot-Product Attention)

2.7.1 缩放点积注意力原理

Transformer 采用一种名为“Scaled Dot-Product Attention（缩放点积注意力）” 的自注意力机制。全局注意力考虑每个单词相对于整个输入序列的重要性，而自注意力则解读序列中单词之间的依赖关系。

例如，在“我去商店买了很多水果和一些家具。它们的味道很棒”这句话中，人类读者会推断“他们”指的是水果，而不是家具。使用全局注意力的模型可能会为“水果”、“家具”和“很棒”分配更高的注意力值，而无需理解这些词之间的关系。相比之下，自注意力将输入序列中的每个单词与其他每个单词进行比较，能够发现“他们”的本意。

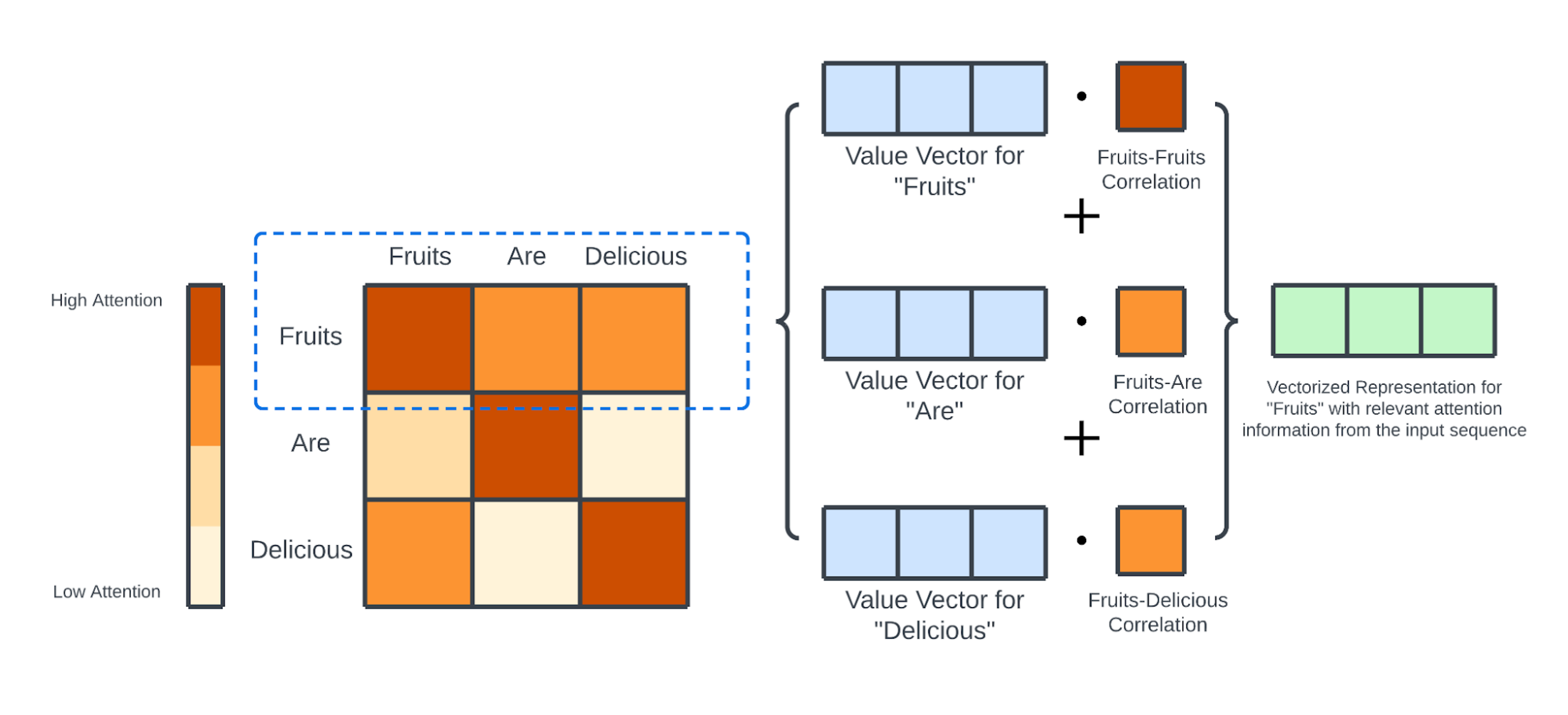
Q查询矩阵 对应的是 Q查询 中单词的矢量化表示，K键矩阵 对应的是 K键 中单词的矢量化表示，所以：
$$
Q \times K = 权重矩阵
$$
即如下图：

二维空间中两个向量之间的点积可以看作是向量之间余弦相似度的度量，由其量级的乘积缩放。

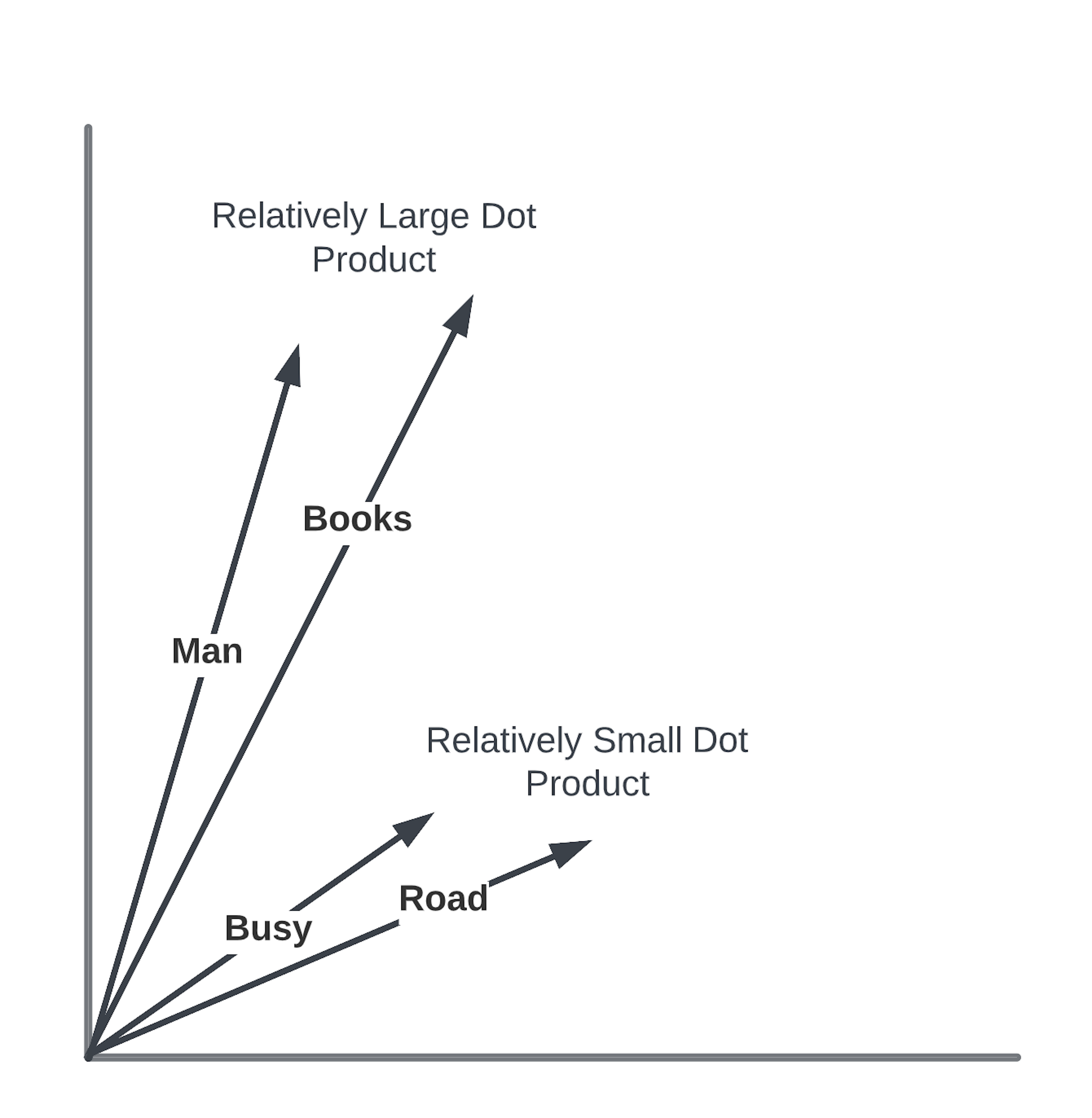
比如，有一个句子：“一个男人走在繁忙的道路上，手里拿着他刚买的几本书。”

我们想要理解这个句子中哪些词对于理解句子的整体含义是最重要的。

2. 词向量表示：将句子中的每个词转换成一个向量。在这个简化的例子中，我们假设每个词的向量是二维的。

3. 选择查询词：我们选择一个词作为“查询”（Q），比如“男人”，我们想要知道这个词在句子中与其他词的关系。

4. 计算相似度：将“男人”的向量与句子中其他词的向量（这里我们把它们当作“键”K）进行比较，比如“书”和“道路”。通过计算向量间的点积来评估它们之间的相似度。

5. 应用注意力权重：根据点积的结果，我们给每个词分配一个权重。如果“男人”和“书”的点积很高，意味着它们之间有很强的关联，因此“书”会得到一个较大的权重。

6. 简化决策：在这个例子中，我们简化了决策过程，认为“男人”和“书”之间的关系比“男人”和“道路”之间的关系更重要，因为“书”直接描述了“男人”的行为。

7. 最终输出：通过加权这些关系，我们可以得到一个综合的表示，这个表示强调了“男人”和“书”之间的关系，而对“男人”和“道路”的关系给予较少的重视。

通过这种方式，注意力机制帮助我们识别和强调句子中最重要的部分，忽略那些可能不那么关键的信息。在这个例子中，它帮助我们集中关注“男人”和“书”，因为它们对于理解句子可能更为重要。

由 Q查询 和 K键 矩阵的点积生成的 注意力权重矩阵 具有 (序列长度，序列长度) 的形状。

注意力权重矩阵 中的每个值都除以 K键、Q查询 和 V值 矩阵大小的平方根（在本例中为 8）。

此步骤用于在训练期间稳定梯度。然后，注意力权重矩阵 通过 softmax 函数，该函数将其值标准化为 0 到 1 之间，并确保矩阵中每行的值总和为 1。

如前所述，使用 注意力值 和 值 向量进行加权求和。将注意力得分归一化为总和为 1 使得这种加权求和运算成为可能。

最后，将归一化的 注意力权重矩阵 与 值矩阵 相加，得到一个大小为 (序列长度，64) 的矩阵，该矩阵可以看作是带有注意力信息的输入序列的较小矢量化表示。

输出矩阵的第一行是V值矩阵中行向量的加权和，权重是输入序列中第一个词对所有其他词的注意力值。

请注意，输出矩阵的大小为 (序列长度，64) 而不是 (序列长度，512)。

重点要记住，输出矩阵的大小应与原始词嵌入相同，因为它将用作下一个编码器层的输入，在第一个编码层的情况下，该编码器层需要将词嵌入作为输入。

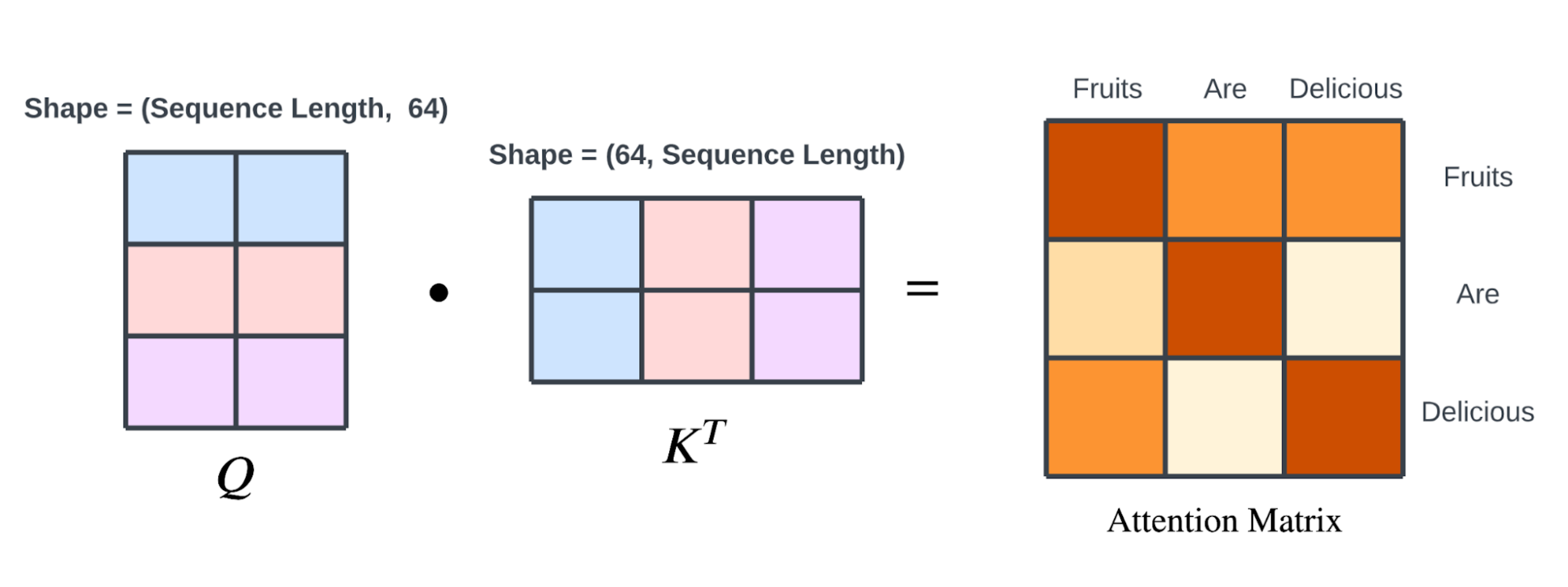
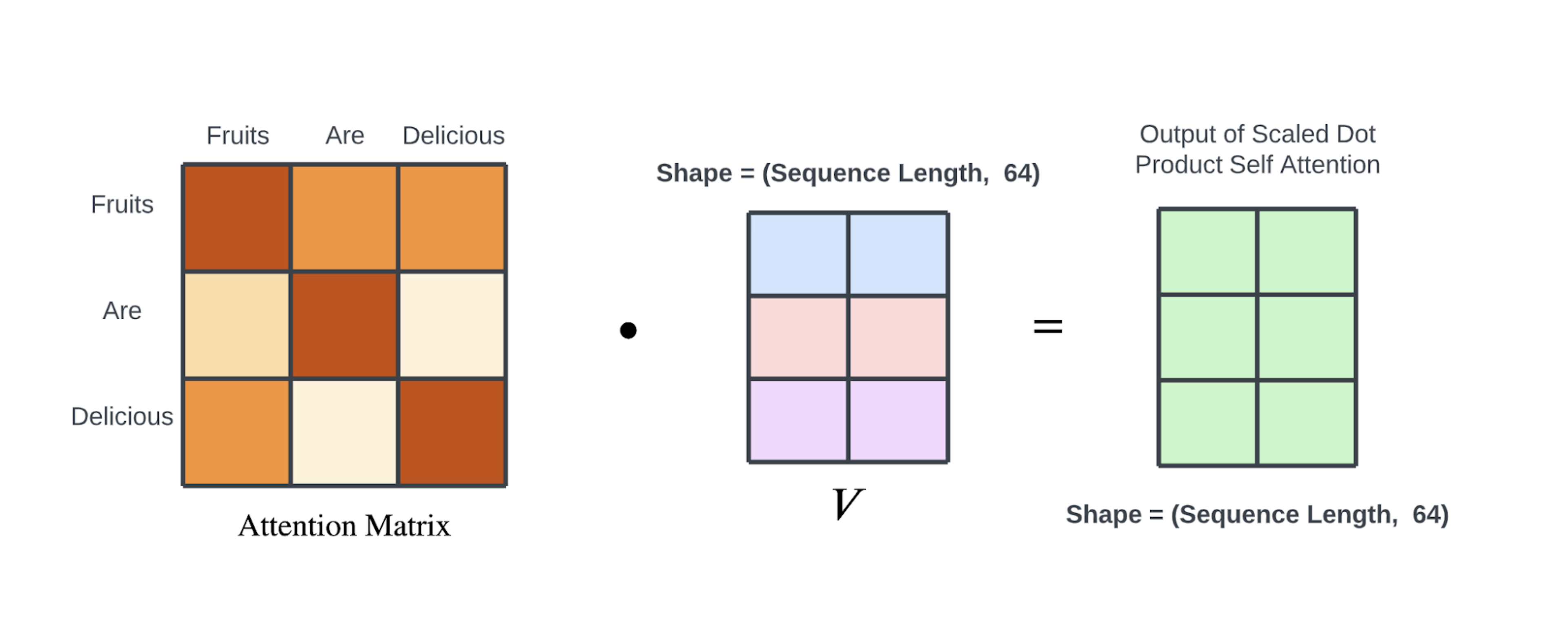
在Transformer中使用的缩放点积注意力权重计算，可以使用查询 $Q(N×D)$ 和输入$K(N×D)$ 以下的公式表示。

在处理问答或机器翻译等任务时，使用Transformer模型，上述公式中的 $Q$ 和 $K$ 分别是表示文章数据的矩阵。

当处理的数据是 “用 $D$ 维词向量表示的 $N$ 个词的文章数据” 时，$Q$ 和 $K$ 是 $N×D$ 大小的矩阵。

因此，这个计算了 查询$Q$ 和 输入数据 $K$ 中的点积。

向量之间的点积大意味着方向接近，即向量之间的相似性高（词之间的相似性高）。也就是说，如果将文章数据输入到ScaledDotProductAttention 中，$Q$ 和 $K$ 中的词之间的相似性将作为输入的重要性进行加权。

通过计算上面得到的注意力权重。该权重 和 值$V$ 的乘积，可以得到最终的输出注意力特征。

2.7.2 代码实现

import numpy as np
import torch
from torch import nn

class ScaledDotProductAttention(nn.Module):
    # 初始化ScaledDotProductAttention类，它是一个PyTorch模型模块
    def __init__(self, d_k: int) -> None:
        super().__init__()  # 调用基类的初始化方法
        self.d_k = d_k  # d_k是输入特征的维度，用于计算缩放因子

    def forward(
        self,
        q: torch.Tensor,  # 查询（Q），一个张量
        k: torch.Tensor,  # 键（K），一个张量
        v: torch.Tensor,  # 值（V），一个张量
        mask: torch.Tensor = None,  # 掩码，用于在计算注意力权重时忽略某些位置，默认为None
    ) -> torch.Tensor:  # 定义forward方法，返回注意力机制的输出
        scalar = np.sqrt(self.d_k)  # 根据d_k计算缩放因子
        # 计算Q和K的点积，然后除以缩放因子，得到未归一化的注意力权重
        attention_weight = torch.matmul(q, torch.transpose(k, 1, 2)) / scalar 

        # 如果提供了掩码，则在计算注意力权重时将掩码位置的权重置为负无穷
        if mask is not None: 
            if mask.dim() != attention_weight.dim():
                raise ValueError(
                    "掩码的维度与注意力权重的维度不匹配，掩码的维度={}, 注意力权重的维度={}".format(
                        mask.dim(), attention_weight.dim()
                    )
                )
            attention_weight = attention_weight.data.masked_fill_(
                mask, -torch.finfo(torch.float).max
            ) 

        # 对未归一化的注意力权重应用softmax函数，得到归一化的注意力权重
        attention_weight = nn.functional.softmax(attention_weight, dim=2) 
        # 计算加权的值，即用归一化的注意力权重乘以V，完成注意力机制的计算
        return torch.matmul(attention_weight, v) 

如果掩码的维度不等于注意力权重的维度，将引发错误。

注意力权重通过softmax函数计算得出：

attention_weight = nn.functional.softmax(attention_weight, dim=2)  # 计算注意力权重

最终，通过注意力权重和 输入X 的乘积得到加权结果：

return torch.matmul(attention_weight, v)  # 通过 (注意力权重) * X 进行加权。

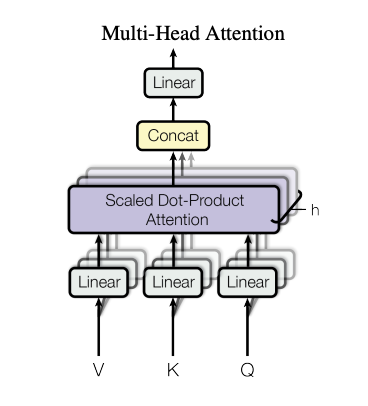
第八节 多头注意力机制

2.8.1 多头注意力机制

在第上一节中，我们解释了Transformer模型使用Scaled Dot-Product Attention作为其注意力计算方法。

然而，Transformer中使用的注意力不仅仅是简单的Scaled Dot-Product Attention，实际上，Transformer采用了一种称为Multihead Attention的机制，它并行地执行多个Scaled Dot-Product Attention。

多头自注意力机制顾名思义就是将多个“注意力头”应用于同一序列。确切的自注意力机制会并行地对同一输入序列重新应用八次。对于每个注意力头，其Q查询、K键和V值权重矩阵 都会随机初始化，期间每个注意力头都能从输入序列中捕获不同类型的信息。

每个注意力头都会产生一个形状为 (序列长度，64) 的矩阵；然后它们沿其第二维连接起来，创建一个形状为 (序列长度，8*64) 的矩阵。在此矩阵上执行线性投影以“结合”所有注意力头的知识。用于线性投影的权重矩阵与模型的其余部分一起通过反向传播进行训练。

让我们来看一下论文中Multihead Attention的示意图。

在 Transformer 的原始论文中，作者使用了 8 个注意力头。但后来的研究表明，这可能没有必要。在论文《分析多头自注意力：专用注意力头承担重任，其余部分可以修剪》中，Elena Voita 等人提出，在 8 个注意力头中，有三个“专用”注意力头承担了大部分工作。具体来说，这些专用注意力头的作用被假设如下：

图中的 $h$(头数) 表示并行运行的 ScaledDotProductAttention 的数量。

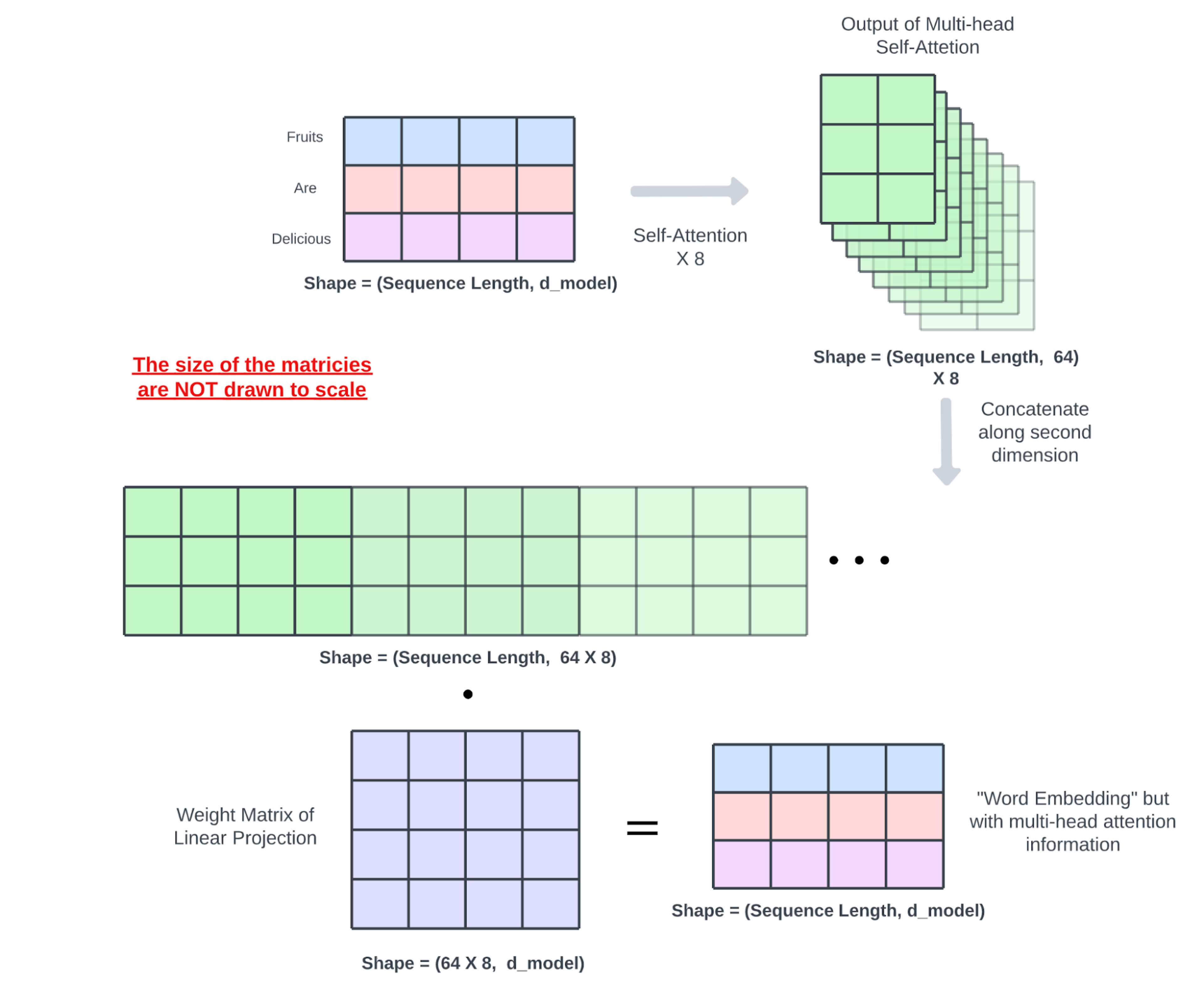
Multihead Attention执行以下处理：

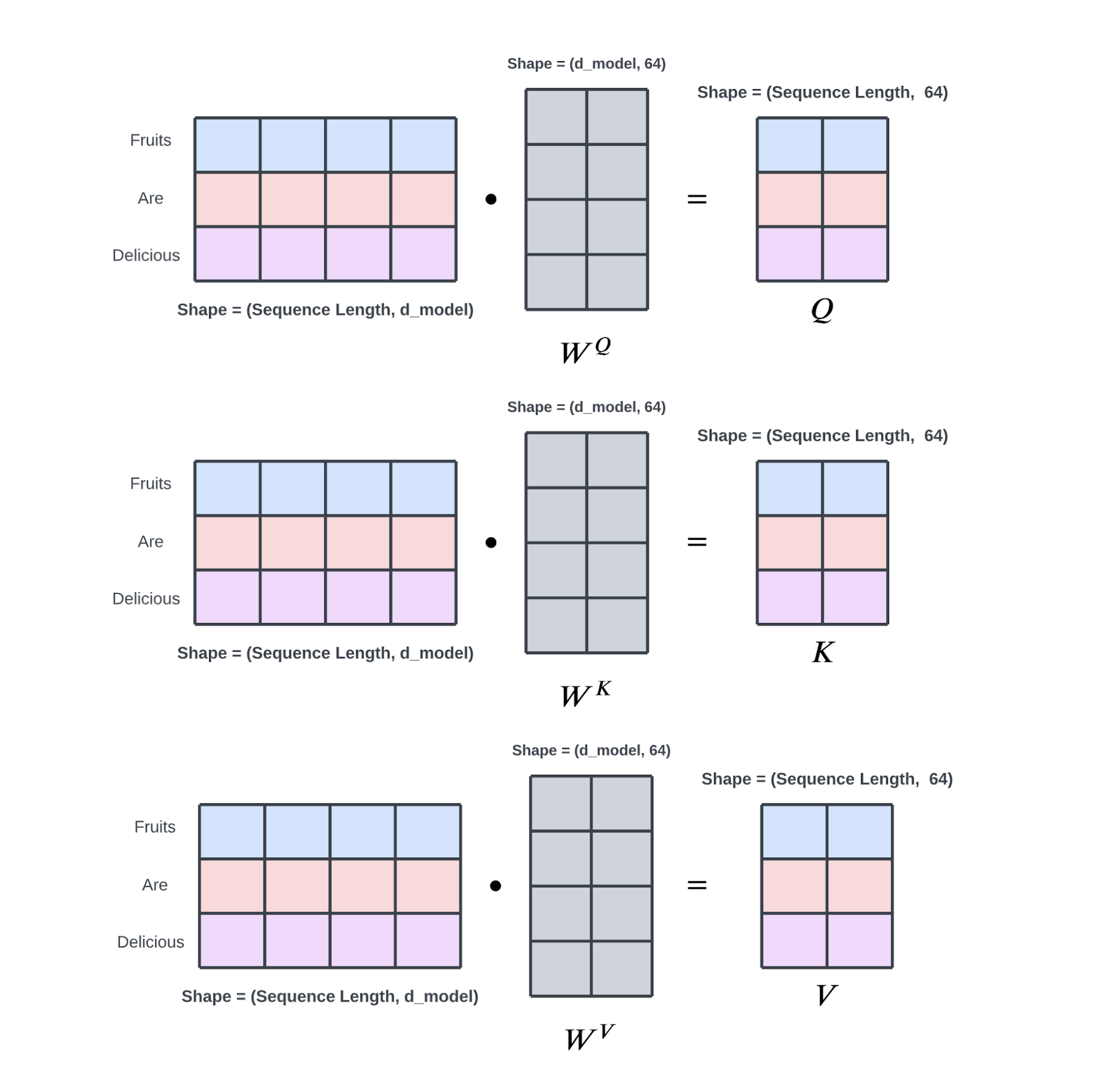
1. 将输入$Q(N_q×d_{model})$、$K(N×d_{model})$、$V(N×d_{model})$复制成 $h$(头数)份。
2. 使用矩阵 $W_i^q(d_{model}×d_k)$、$W_i^k(d_{model}×d_k)$、$W_i^v(d_{model}×d_v)$ 将复制的输入 $Q_i$、$K_i$、$V_i$ 分别线性变换为$d_{model}→d_v,d_k$。
3. 将获得的 $Q_iW_i^q$、$K_iW_i^k$、$V_iW_i^v$ 输入到 $h$ 个存在的 ScaledDotProductAttention 中。
4. 将并行运行的 ScaledDotProductAttention 得到的 $h$ 个输出头 $head(i=1 \sim h,N×d_v)$ 连接(concat)起来，得到矩阵$O(N×hd_v)$。
5. 使用 $OW^O$ 将 $O$ 从 $hd_v$ 变换到 $d_{model}$ ，得到的值作为最终输出。

公式化表示如下：
$$
\text{head}_i = \text{ScaledDotProductAttention}(Q_iW_i^q, K_iW_i^k, V_iW_i^v) \quad (i=1\sim h)
$$

$$
O = \text{Concat}(\text{head}_1, …, \text{head}_h)
$$
$$
\text{MultiHead}(Q, K, V) = O W^O
$$

2.8.2 代码实现

import torch
from layers.transformer.ScaledDotProductAttention import ScaledDotProductAttention
from torch import nn

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model: int, h: int) -> None:
        super().__init__()
        self.d_model = d_model
        self.h = h
        self.d_k = d_model // h
        self.d_v = d_model // h

        # 定义参数矩阵
        self.W_k = nn.Parameter(
            torch.Tensor(h, d_model, self.d_k)  # 头数, 输入维度, 输出维度(=输入维度/头数)
        )

        self.W_q = nn.Parameter(
            torch.Tensor(h, d_model, self.d_k)  # 头数, 输入维度, 输出维度(=输入维度/头数)
        )

        self.W_v = nn.Parameter(
            torch.Tensor(h, d_model, self.d_v)  # 头数, 输入维度, 输出维度(=输入维度/头数)
        )

        self.scaled_dot_product_attention = ScaledDotProductAttention(self.d_k)

        self.linear = nn.Linear(h * self.d_v, d_model)

    def forward(
        self,
        q: torch.Tensor,
        k: torch.Tensor,
        v: torch.Tensor,
        mask_3d: torch.Tensor = None,
    ) -> torch.Tensor:

        batch_size, seq_len = q.size(0), q.size(1)

        # 按头数重复Query, Key, Value
        q = q.repeat(self.h, 1, 1, 1)  # head, batch_size, seq_len, d_model
        k = k.repeat(self.h, 1, 1, 1)  # head, batch_size, seq_len, d_model
        v = v.repeat(self.h, 1, 1, 1)  # head, batch_size, seq_len, d_model

        # 在缩放点积注意力之前进行线性变换
        q = torch.einsum(
            "hijk,hkl->hijl", (q, self.W_q)
        )  # head, batch_size, d_k, seq_len
        k = torch.einsum(
            "hijk,hkl->hijl", (k, self.W_k)
        )  # head, batch_size, d_k, seq_len
        v = torch.einsum(
            "hijk,hkl->hijl", (v, self.W_v)
        )  # head, batch_size, d_k, seq_len

        # 分割头
        q = q.view(self.h * batch_size, seq_len, self.d_k)
        k = k.view(self.h * batch_size, seq_len, self.d_k)
        v = v.view(self.h * batch_size, seq_len, self.d_v)

        if mask_3d is not None:
            mask_3d = mask_3d.repeat(self.h, 1, 1)

        # 缩放点积注意力
        attention_output = self.scaled_dot_product_attention(
            q, k, v, mask_3d
        )  # (head*batch_size, seq_len, d_model)

        attention_output = torch.chunk(attention_output, self.h, dim=0)
        attention_output = torch.cat(attention_output, dim=2)

        # 在缩放点积注意力之后进行线性变换
        output = self.linear(attention_output)
        return output

第九节 位置前馈网络

Position-wise Feed-Forward Networks（FFN）是一个非常简单的层，只包含两个全连接层（Linear）。在第一个层的输出上使用ReLU作为激活函数。

Position-wise Feed-Forward Networks（FFN）的公式化表示如下：
$$
FFN(x) = \max(0, xW_1 + b_1)W_2 + b_2
$$

接下来，让我们看看实现。

import torch
from torch import nn
from torch.nn.functional import relu

class FFN(nn.Module):
    def __init__(self, d_model: int, d_ff: int) -> None:
        super().__init__()
        self.linear1 = nn.Linear(d_model, d_ff)
        self.linear2 = nn.Linear(d_ff, d_model)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return self.linear2(relu(self.linear1(x)))

第十节 Transformer完整实现

到目前为止，我们已经完成了构成Transformer的各个部分的实现，包括Attention、PositionalEncoding、Encoder和Decoder。本章我们将转移到实现Transformer本身。

但事实上，由于Encoder和Decoder的实现已经完成，模型的实现本身非常简单，只需要将这两者结合起来即可。接下来，让我们看看实现。

import torch
from layers.transformer.TransformerDecoder import TransformerDecoder
from layers.transformer.TransformerEncoder import TransformerEncoder
from torch import nn

class Transformer(nn.Module):
    # Transformer模型的初始化方法
    def __init__(
        self,
        src_vocab_size: int,                         # 源语言词汇表大小
        tgt_vocab_size: int,                         # 目标语言词汇表大小
        max_len: int,                                # 输入序列的最大长度
        d_model: int = 512,                          # 模型的维度
        heads_num: int = 8,                          # 多头注意力中头的数量
        d_ff: int = 2048,                            # 馈前网络的维度
        N: int = 6,                                  # 编码器和解码器层的数量
        dropout_rate: float = 0.1,                   # dropout率
        layer_norm_eps: float = 1e-5,                # LayerNorm的epsilon值
        pad_idx: int = 0,                            # 填充索引
        device: torch.device = torch.device("cpu"),  # 指定设备，默认为CPU
    ):
        super().__init__()  # 调用基类的初始化方法

        # 初始化模型参数
        self.src_vocab_size = src_vocab_size
        self.tgt_vocab_size = tgt_vocab_size
        self.d_model = d_model
        self.max_len = max_len
        self.heads_num = heads_num
        self.d_ff = d_ff
        self.N = N
        self.dropout_rate = dropout_rate
        self.layer_norm_eps = layer_norm_eps
        self.pad_idx = pad_idx
        self.device = device

        # 初始化Transformer的编码器
        self.encoder = TransformerEncoder(
            # 编码器初始化参数
            src_vocab_size,
            max_len,
            pad_idx,
            d_model,
            N,
            d_ff,
            heads_num,
            dropout_rate,
            layer_norm_eps,
            device,
        )

        # 初始化Transformer的解码器
        self.decoder = TransformerDecoder(
            # 解码器初始化参数
            tgt_vocab_size,
            max_len,
            pad_idx,
            d_model,
            N,
            d_ff,
            heads_num,
            dropout_rate,
            layer_norm_eps,
            device,
        )

        # 初始化输出层的线性变换
        self.linear = nn.Linear(d_model, tgt_vocab_size)

    # Transformer模型的前向传播方法
    def forward(self, src: torch.Tensor, tgt: torch.Tensor) -> torch.Tensor:
        """
        参数:
        ----------
        src : torch.Tensor
            单词的ID序列，形状为[batch_size, max_len]
        tgt : torch.Tensor
            单词的ID序列，形状为[batch_size, max_len]
        """

        # 创建源序列的padding掩码
        pad_mask_src = self._pad_mask(src)

        # 编码器处理源序列
        src = self.encoder(src, pad_mask_src)

        # 创建解码器的掩码，结合了后续掩码和padding掩码
        mask_self_attn = torch.logical_or(
            self._subsequent_mask(tgt), self._pad_mask(tgt)
        )
        # 解码器处理目标序列
        dec_output = self.decoder(tgt, src, pad_mask_src, mask_self_attn)

        # 通过输出层的线性变换
        return self.linear(dec_output)

    # 创建源序列的padding掩码
    def _pad_mask(self, x: torch.Tensor) -> torch.Tensor:
        """根据单词的ID序列创建padding掩码。
        参数:
        ----------
        x : torch.Tensor
            单词的ID序列，形状为[batch_size, max_len]
        """
        # 计算序列长度
        seq_len = x.size(1)
        # 创建一个与序列长度相同的padding掩码，padding位置为True
        mask = x.eq(self.pad_idx)  # 0是词汇表中的<pad>标记
        mask = mask.unsqueeze(1)  # 增加一个维度以匹配序列长度
        mask = mask.repeat(1, seq_len, 1)  # 复制掩码以匹配序列长度
        # 将掩码移动到指定的设备
        return mask.to(self.device)

    # 创建解码器的后续掩码
    def _subsequent_mask(self, x: torch.Tensor) -> torch.Tensor:
        """为解码器的Masked-Attention创建掩码。
        参数:
        ----------
        x : torch.Tensor
            单词的token序列，形状为[batch_size, max_len, d_model]
        """
        # 获取批次大小和序列最大长度
        batch_size = x.size(0)
        max_len = x.size(1)
        # 创建一个下三角矩阵，用于在解码器中防止未来信息的泄露
        return (
            torch.tril(torch.ones(batch_size, max_len, max_len)).eq(0).to(self.device)
        )

第十一节 Transformer训练

现在我们已经实现了Transformer，接下来我们将使用实际的机器翻译数据集来训练它。

为了训练模型，我们在train.py中定义了一个名为Trainer的类，用于训练。

Trainer类参考了PyTorch Lightning的API，包含以下五个方法：

• loss_fn: 计算损失函数
• train_step: 训练中的单步（训练）
• val_step: 训练中的单步（验证）
• fit: 通过批量学习进行模型的训练和验证
• test: 使用测试数据进行模型验证

那么我们来看看它的实现。 Trainer类的实现如下。

from os.path import join
from typing import List, Tuple
import torch
from matplotlib import pyplot as plt
from torch import nn, optim
from torch.utils.data import DataLoader

# 导入自定义模块和常量
from const.path import FIGURE_PATH, KFTT_TOK_CORPUS_PATH, NN_MODEL_PICKLES_PATH, TANAKA_CORPUS_PATH
from models import Transformer
from utils.dataset.Dataset import KfttDataset
from utils.evaluation.bleu import BleuScore
from utils.text.text import tensor_to_text, text_to_tensor
from utils.text.vocab import get_vocab

class Trainer:
    def __init__(
        self,
        net: nn.Module,
        optimizer: optim.Optimizer,
        criterion: nn.Module,  # 修正了变量名拼写错误
        bleu_score: BleuScore,
        device: torch.device,
    ) -> None:
        # 初始化训练器
        self.net = net.to(device)  # 将模型移动到设备上
        self.optimizer = optimizer
        self.criterion = criterion  # 修正了变量名拼写错误
        self.device = device
        self.bleu_score = bleu_score

    def loss_fn(self, preds: torch.Tensor, labels: torch.Tensor) -> torch.Tensor:
        # 定义损失函数
        return self.criterion(preds, labels)

    def train_step(self, src: torch.Tensor, tgt: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor, float]:
        # 单步训练过程
        self.net.train()  # 设置模型为训练模式
        output = self.net(src, tgt)

        # 调整目标和预测输出的形状以计算损失
        tgt = tgt[:, 1:]  # 忽略序列的第一个元素（通常是<BOS>）
        output = output[:, :-1, :]

        loss = self.loss_fn(
            output.contiguous().view(-1, output.size(-1)),
            tgt.contiguous().view(-1)
        )

        # 计算BLEU分数
        _, output_ids = torch.max(output, dim=-1)
        bleu_score = self.bleu_score(tgt, output_ids)

        self.optimizer.zero_grad()  # 清除之前的梯度
        loss.backward()             # 反向传播
        self.optimizer.step()       # 更新参数

        return loss, output, bleu_score

    def val_step(self, src: torch.Tensor, tgt: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor, float]:
        # 单步验证过程
        self.net.eval()  # 设置模型为评估模式
        output = self.net(src, tgt)

        tgt = tgt[:, 1:]
        output = output[:, :-1, :]

        loss = self.loss_fn(
            output.contiguous().view(-1, output.size(-1)),
            tgt.contiguous().view(-1)
        )

        _, output_ids = torch.max(output, dim=-1)
        bleu_score = self.bleu_score(tgt, output_ids)

        return loss, output, bleu_score

    def fit(self, train_loader: DataLoader, val_loader: DataLoader, print_log: bool = True):
        # 训练和验证过程
        train_losses, train_bleu_scores = [], []
        if print_log:
            print(f"{'-'*20} Train {'-'*20}")

        for i, (src, tgt) in enumerate(train_loader):
            src, tgt = src.to(self.device), tgt.to(self.device)
            loss, _, bleu_score = self.train_step(src, tgt)
            src, tgt = src.to("cpu"), tgt.to("cpu")

            if print_log:
                print(f"train loss: {loss.item()}, bleu score: {bleu_score}, iter: {i+1}/{len(train_loader)}")

            train_losses.append(loss.item())
            train_bleu_scores.append(bleu_score)

        val_losses, val_bleu_scores = [], []
        if print_log:
            print(f"{'-'*20} Validation {'-'*20}")

        for i, (src, tgt) in enumerate(val_loader):
            src, tgt = src.to(self.device), tgt.to(self.device)
            loss, _, bleu_score = self.val_step(src, tgt)
            src, tgt = src.to("cpu"), tgt.to("cpu")

            if print_log:
                print(f"val loss: {loss.item()}, iter: {i+1}/{len(val_loader)}")

            val_losses.append(loss.item())
            val_bleu_scores.append(bleu_score)

        return train_losses, train_bleu_scores, val_losses, val_bleu_scores

    def test(self, test_data_loader: DataLoader) -> Tuple[List[float], List[float]]:
        # 测试过程
        test_losses, test_bleu_scores = [], []
        for i, (src, tgt) in enumerate(test_data_loader):
            src, tgt = src.to(self.device), tgt.to(self.device)
            loss, _, bleu_score = self.val_step(src, tgt)  # 这里应该使用测试步骤，而不是验证步骤
            src, tgt = src.to("cpu"), tgt.to("cpu")

            test_losses.append(loss.item())
            test_bleu_scores.append(bleu_score)

        return test_losses, test_bleu_scores

现在我们来训练一下模型。运行以下命令来训练模型。

poetry run python train.py

第十二节 总结

Transformer模型推出自2017以来已有多年时间，所以不能简单地将其视为一个全新的模型。尽管如此，在近期的自然语言处理技术发展中，大多数被认为是技术前沿（SoTA）的模型都是基于Transformer或注意力（Attention）机制构建的。

因此，Transformer无疑成为了理解深度学习最新进展的一个关键性模型。

随着相关库的日益完善，构建像Transformer这样复杂的模型变得更加容易，进入门槛也相应降低。然而，我坚信深入了解模型的内部结构对于提升我们的实际应用能力至关重要。如果你对此感兴趣，我鼓励你亲自尝试实现这些模型，即便这可能意味着要重新发明一些已经存在的概念。

第三章 实验

参考：

https://www.datacamp.com/tutorial/building-a-transformer-with-py-torch

https://github.com/YadaYuki/en_ja_translator_pytorch/tree/master

https://github.com/karpathy/nanoGPT

换源

[tool.poetry]
name = "en_ja_translator_pytorch"
version = "0.1.0"
description = ""
authors = ["YadaYuki <yada.yuki@fuji.waseda.jp>"]

[[tool.poetry.source]]
name = "aliyun"
url = "http://mirrors.aliyun.com/pypi/simple"
default = true

[tool.poetry.dependencies]
python = "^3.8"
requests = "^2.27.1"
scikit-learn = "^1.0.2"
torch = "^1.10.2"
pytest = "^7.0.1"
matplotlib = "^3.5.1"
sklearn = "^0.0"
torchtext = "^0.12.0"

[tool.poetry.dev-dependencies]
mypy = "^0.931"
isort = "^5.10.1"
flake8 = "^4.0.1"
black = "^22.1.0"
types-requests = "^2.27.10"

[build-system]
requires = ["poetry-core>=1.0.0"]
build-backend = "poetry.core.masonry.api"

阅读扩展

第一节 Transformer中Add、Norm和前馈网络

在 Transformer 模型中，多头注意力模块的输出通过层归一化组件进行处理。

层归一化应用于编码器层的输入，有助于确保输入具有一致的分布，从而提高模型的稳定性和训练速度。

具体来说，归一化将输入数据的均值和方差调整到标准范围，这减少了数据分布的波动，提高了模型训练的效率。

1.1 层归一化

Layer Normalization（层归一化）的主要作用是在深度神经网络中稳定和加速训练过程。它通过标准化每一层的输入，减轻了内部协变量转移（Internal Covariate Shift）的问题。具体作用和实现如下：

作用：

1. 稳定训练过程：

   • Layer Normalization通过对每个样本的特征进行归一化，使得每层的输入具有相似的分布。这有助于在训练过程中使梯度的变化更加平滑和稳定，减轻梯度爆炸或消失的问题。

2. 加速收敛：

   • 归一化可以使模型的优化过程更高效，从而加速收敛。模型的参数更新更趋于稳定，训练速度更快。

3. 减少依赖于批大小：

   • 与Batch Normalization不同，Layer Normalization是对单个样本的特征进行归一化，而不是对整个mini-batch进行归一化。这使得它在处理小批量数据甚至单个样本时表现更好，更加稳定。

4. 提高模型的泛化能力：

   • 通过减少特征间的相互依赖性，Layer Normalization有助于提高模型在未见数据上的表现，增强模型的泛化能力。

实现:

Layer Normalization对每个样本的特征进行归一化处理，即对于一个输入向量 $ x = (x_1, x_2, \ldots, x_n) $，其归一化公式如下：

$$
\hat{x}_i = \frac{x_i - \mu}{\sigma} \cdot \gamma + \beta
$$

其中：

• $ \mu $ 是输入向量的均值：
  $$
  \mu = \frac{1}{n} \sum_{i=1}^{n} x_i
  $$
• $ \sigma $ 是输入向量的标准差：
  $$
  \sigma = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2}
  $$
• $ \gamma $ 和 $ \beta $ 是可训练的缩放和平移参数。

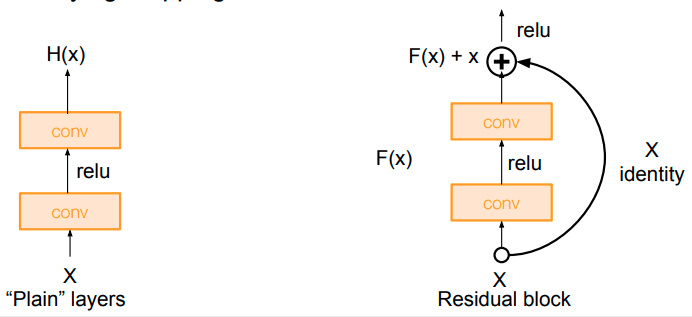
1.2 残差连接的作用

层归一化组件还引入了残差连接，允许将输入直接添加到归一化层的输出。

这种残差连接改善了训练期间梯度的流动，使得梯度更容易反向传播，从而提高训练的稳定性和速度。

残差连接通过绕过某些层将输入直接传递到后面的层，有助于减缓梯度消失问题，并使得更深层次的神经网络能够有效训练。

1.3 前馈网络与最终编码表示

归一化后的输出会通过一个浅层三层前馈网络进行处理，该网络生成输入序列的最终编码表示。

这个前馈网络包括两个线性变换和一个 ReLU 激活函数：

1. 第一层线性变换：将输入映射到高维空间（通常为 2048 个神经元）。
2. ReLU 激活函数：引入非线性，使得模型能够捕捉到数据中的复杂关系。
3. 第二层线性变换：将高维空间的表示映射回输入的原始维度（通常为 512 个神经元）。

前馈网络的目的是在局部进行深度特征提取，增强模型的表示能力。经过前馈网络处理后的输出，再次经过层归一化和残差连接（Add & Norm），进一步稳定了训练过程。

1.4 编码层的整体架构

在 Transformer 模型的编码层中，输入和输出都具有 $d_{model}$个神经元，原始论文中设定为 512 个。中间隐藏层通常有 2048 个神经元。这种设计确保了模型在捕捉复杂特征的同时，保持计算效率。

综上所述，通过层归一化、残差连接和前馈网络的结合，Transformer 模型能够实现高效、稳定的训练，生成精确的输入序列编码表示。这些组件相互协作，共同提升了模型的性能和训练效果。

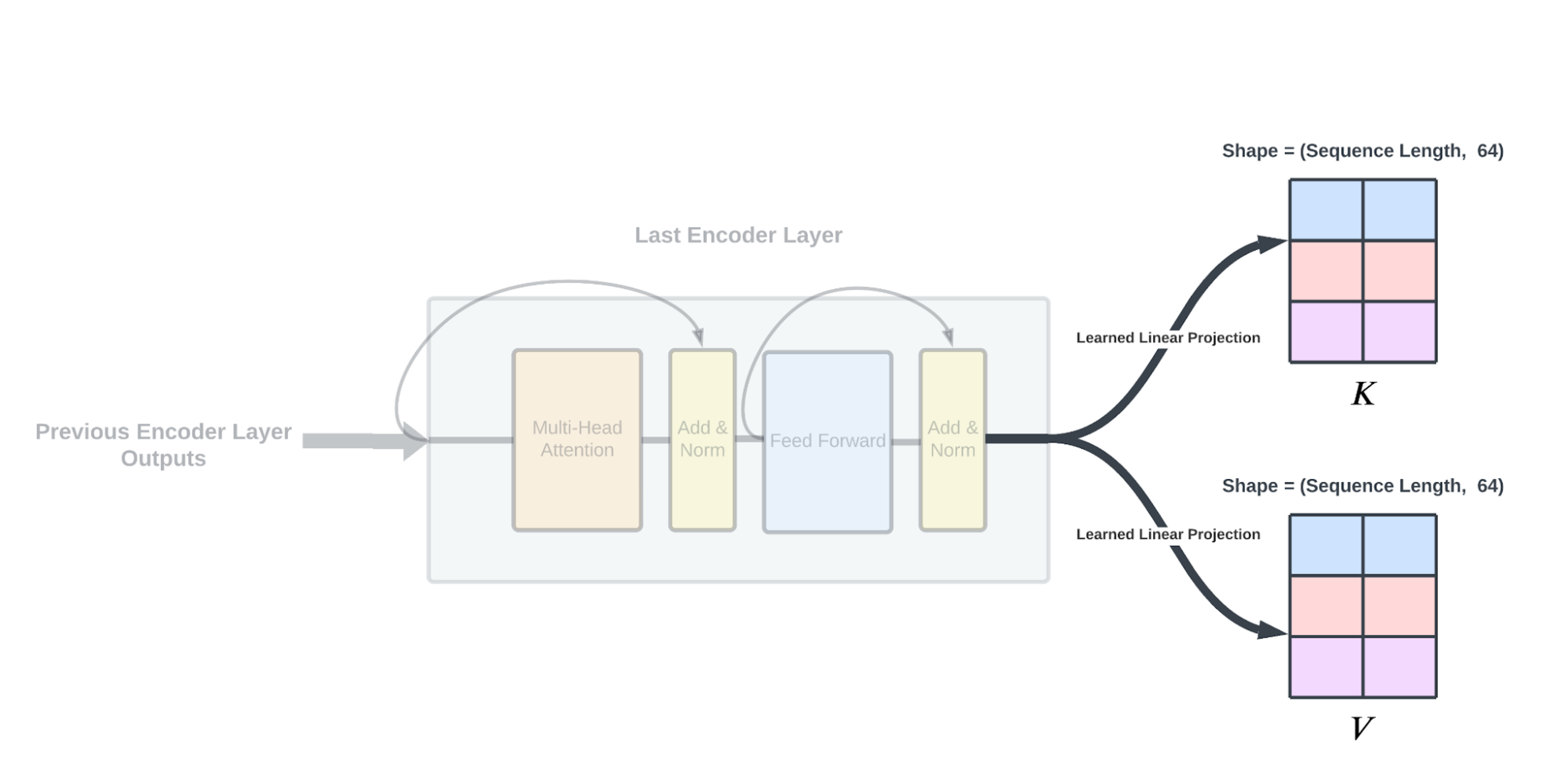
第二节 编码器输出

最后一个编码器层的输出经过另一组通过反向传播学习的线性投影，类似于在自注意力模块中执行的线性投影，从而产生一个键和一个值矩阵以输入到解码器中。

在对编码器方面进行详尽解释之后，让我们深入研究解码器。

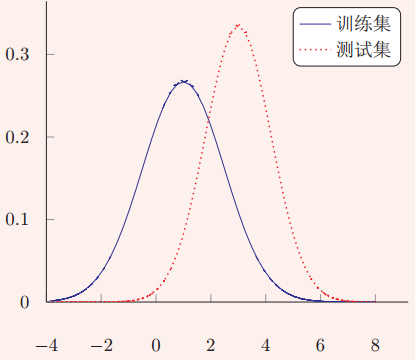
第三节 内部协变量偏移问题的产生

在传统机器学习领域中，常常会碰到协变量偏移这一普遍问题。简单来说，就是数据往往会伴随时间推移而发生变动，当利用基于旧数据训练好的模型去对新数据进行预测时，其所得结果或许就会缺乏准确性。

将输入数据视作协变量的话，那么机器学习算法就会要求输入数据在训练集与测试集上能够达到相同的分布状态，只有这样，当运用该模型去对新数据进行预测时，才有可能收获较为理想的效果。

在深层神经网络中，内部协变量偏移（Internal Covarian Shift）可拆成“中间”与“协变量偏移”来解读。

“中间”意味着神经网络的中间层，也就是隐藏层，

“协变量偏移“与传统机器学习的概念相仿。于深层神经网络而言，中间层的输入等于前一层的输出，前一层参数的变化会使中间层输入 $WU+b$ 的分布出现显著差异。当利用随机梯度下降训练网络时，每次参数更新都会引起中间层输入分布的改变，进而导致同一迭代中各中间层的输入分布不一致，不同迭代轮次中同一中间层的输入分布也会发生变化，这就是内部协变量偏移情况。传统机器学习的协变量偏移是因为测试集和训练集中输入分布不相同，而深层神经网络的内部协变量偏移则是不同中间层输入分布的不一致。