全连接网络与基础应用

常见模型：线性回归与逻辑回归

机器学习（Machine Learning）是人工智能（Artificial Intelligence）的一个重要领域，主要涉及使用算法和模型来识别模式、做出预测和决策。根据学习方式和任务的不同，机器学习主要分为以下几个主要类别：

1. 监督学习（Supervised Learning）：在监督学习中，模型从已标注（带有答案）的训练数据中学习，旨在找到输入和输出变量之间的映射关系。

2. 无监督学习（Unsupervised Learning）：无监督学习模型试图从未标注的数据中找到隐藏的结构或规律，而不依赖已知答案的标签。

3. 强化学习（Reinforcement Learning）：在强化学习中，智能体通过与环境的交互学习如何执行任务或实现目标。与传统监督学习不同，强化学习关注一系列的动作和奖励，而不仅仅是单一的输入-输出对。

这些机器学习类别提供了不同的方法和工具，以应对各种类型的问题，从有监督学习用于分类和回归任务，无监督学习用于聚类和降维，到强化学习用于决策和控制。这多样性使机器学习成为解决各种复杂问题的强大工具。

图1 机器学习分类

机器学习常见的算法：

算法	训练方式	简述
线性回归（Linear Regression）	监督学习	线性回归是一种用于建模和预测连续数值输出的监督学习算法。它试图通过线性关系来拟合输入特征和输出之间的关系。
逻辑回归（Logistic Regression）	监督学习	逻辑回归是用于解决二元分类问题的监督学习算法。它使用逻辑函数来估计输入特征和输出之间的概率关系。
线性判别分析（Linear Discriminant Analysis）	监督学习	线性判别分析是一种监督学习算法，主要用于多类别分类问题。它试图在不同类别之间找到最佳线性分隔面。
决策树（Decision Trees）	监督学习	决策树是一种非常直观的监督学习算法，用于分类和回归。它以树形结构表示决策规则，便于理解和解释。
朴素贝叶斯（Naive Bayes）	监督学习	朴素贝叶斯是一种基于贝叶斯定理的分类算法。它假设输入特征之间相互独立，尽管这个假设通常是不现实的。
K 邻近（K-Nearest Neighbors）	监督学习	K 邻近是一种基于实例的监督学习算法，用于分类和回归。它根据最近的 K 个邻居的标签来做出预测。
学习向量量化（Learning Vector Quantization）	监督学习	学习向量量化是一种无监督学习算法，用于将输入数据分组成不同的簇或类别，类似于K均值聚类。
支持向量机（Support Vector Machine）	监督学习	支持向量机是一种强大的监督学习算法，用于分类和回归。它试图找到最佳的分隔超平面，使类别之间的间隔最大化。
随机森林（Random Forest）	监督学习	随机森林是一种集成学习算法，它结合多个决策树来提高分类和回归的性能。
AdaBoost（Adaptive Boosting）	监督学习	AdaBoost是另一种集成学习算法，它通过迭代训练多个弱分类器来提高模型的性能。
高斯混合模型（Gaussian Mixture Model）	非监督学习	高斯混合模型是一种用于聚类和密度估计的算法，它假定数据是由多个高斯分布组成的混合体。
限制波尔兹曼机（Restricted Boltzmann Machine）	非监督学习	限制波尔兹曼机是一种神经网络模型，用于学习数据中的特征和模式。
K-means 聚类（K-means Clustering）	非监督学习	K-means是一种无监督学习算法，用于将数据点划分成 K 个簇，其中每个数据点属于与其最近的质心。
最大期望算法（Expectation-Maximization）	非监督学习	最大期望算法是一种用于估计包含隐变量的概率模型参数的迭代优化算法，常用于高斯混合模型等。

表2 机器学习常见的算法

这些算法各自适用于不同类型的问题和数据，具有各自的特点和应用领域。选择适当的算法取决于具体问题和数据的性质。

线性回归概述

“线性回归”这个名词由两部分组成：一是“线性”（Linear），二是“回归”（Regression）。这两个词都具有特定的统计和数学含义，联合起来构成了线性回归的基本概念，它是一种用于建模和预测变量之间线性关系的统计方法。

首先，让我们了解一下“回归”这个词。在统计学中，回归分析是一种用于建模和分析变量之间关系的方法，尤其是一个或多个自变量和因变量之间的关系。简而言之，回归模型目的是用数学方式解释或预测因变量的变化。例如，如果您有兴趣了解身高和体重之间的关系，回归分析可以用于预测或解释体重（因变量）如何随身高（自变量）的变化而变化。

其次，我们来考察“线性”这个概念。在数学和统计学中，线性表示成比例的或直线的关系，即当你改变一个变量时，另一个变量以固定比率发生变化。换句话说，线性关系可以用直线方程来表示。

线性方程的一般形式如式3所示：
$$
y = w \cdot x+b
$$

式3

其中$y$是因变量，$x$是自变量，$w$是斜率，$b$是截距。这个方程描述了$y$如何随$x$线性变化。斜率$w$表示$x$每改变一个单位时，$y$改变的量，而截距$b$表示当$x$为0时$y$的值。为了给大家更直观感受，我们假定 w=1，b=1，画出这个函数图，如图4所示：

图4

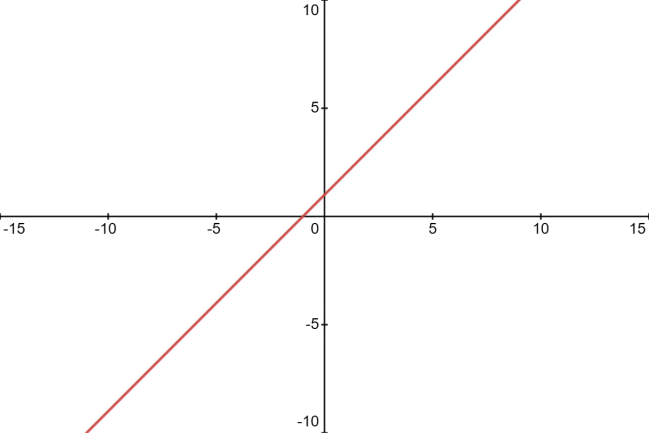
结合这两者，线性回归就是使用线性方程来建模因变量和n个自变量之间的关系。在单变量线性回归中，我们有一个自变量和一个因变量，目标是找到最佳拟合的直线。在多元线性回归中，有两个或以上自变量，目标是找到最佳拟合的超平面。这里所谓拟合就是找到符合需求的合适的$w$和$b$值，让假定的函数近似真实函数，最后我们就可以使用这个函数去做推理预测。

逻辑回归概述

尽管逻辑回归（Logistic Regression）的名称中包含“回归”一词，但它通常用于处理分类问题，尤其是二分类问题。在这里，“回归”和“逻辑”这两个词汇都有其具体的含义。

在统计学和机器学习领域，通常情况下，“回归”用于指代预测数值型目标变量（也叫因变量或输出变量），并建立与一个或多个数值型或类别型特征变量（也叫自变量或输入变量）之间的关系。在逻辑回归中，尽管最终做的任务可能是分类（例如，将一封电子邮件归类为垃圾邮件或非垃圾邮件），但模型内部实际上进行的是数值预测。具体，它预测的是属于某一类的概率，而不是直接预测类别标签。

逻辑回归中的“逻辑”一词源自“逻辑斯蒂函数”（Logistic Function），也称为Sigmoid函数。这是一种S形曲线函数，其数学表达式如式5所示：
$$
σ(z)=\frac{1}{1+e^{-x}}
$$

式5 Sigmoid函数

这个函数在逻辑回归中扮演着重要角色，如图6所示，Sigmoid函数将数值映射到0和1之间，用于表示分类的概率。这种概率模型使逻辑回归成为一种强大的工具，用于解决分类问题。

图6 Sigmoid曲线

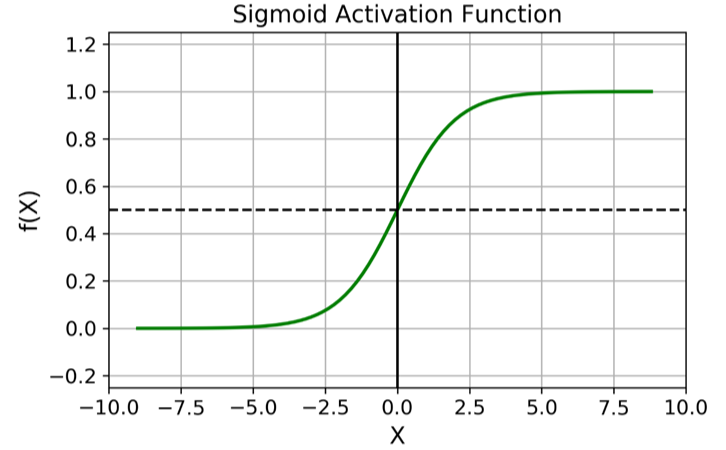
结合两者，逻辑回归是这样工作的：首先进行线性回归预测；然后通过Sigmoid函数将线性预测值转换为概率；最后，根据得到的概率值进行分类。通常，如果概率值大于0.5，就分类为“正类”（例如，是垃圾邮件）；否则，就分类为“负类”（例如，不是垃圾邮件）。这样，逻辑回归既考虑了“回归”（通过线性回归预测数值），又引入了“逻辑”（通过Sigmoid函数将数值转换为概率），从而用于解决分类问题。

线性模型与逻辑模型的区别与联系

线性回归和逻辑回归是统计学和机器学习中两种基础的算法，它们有不少相似之处，但也有关键的不同。下面就来详细探讨一下它们各自的特点以及二者之间的关联。

它们之间的区别：
目标和应用场景
线性回归：用于解决回归问题，即预测一个连续的输出变量（也称为因变量或目标变量）。
逻辑回归：虽然名字里有“回归”，但实际上常用于解决分类问题，特别是二分类问题。

数学表达形式
线性回归：输出是输入特征的线性组合。
逻辑回归：首先计算特征的线性组合，然后通过逻辑函数将这个值映射到 (0, 1) 区间，以表示概率。

输出类型
线性回归：输出是一个任意实数，通常用于表示某种数量（如价格、重量等）。
逻辑回归：输出是一个位于0和1之间的概率值。

损失函数
线性回归：通常使用均方误差（Mean Squared Error, MSE）作为损失函数。
逻辑回归：通常使用交叉熵（Cross Entropy）作为损失函数。

它们之间的联系：逻辑回归在某种程度上可以看作是线性回归的一个扩展。逻辑回归中包含了计算特征的线性组合这一步，但接着又多了一个逻辑函数来进行概率转换。
总体来说，线性回归和逻辑回归在形式和用途上各有侧重，但它们都是从线性模型这个大家族中派生出来的，因此具有一定的内在联系。

损失函数、梯度下降、学习率

在上一节，我们提到过损失函数，那损失函数到底是什么，我们是要使用损失函数呢？为了解释清楚这个问题，我们拿打车需求来说，我们已知如下的打车距离与对应费用的数据，如表7：

距离（公里）	费用（元）
1	15
2	18
3	21
4	24
5	27
6	30
7	33
8	36
9	39
10	42
11	45
12	48
13	51
14	54
15	57

图7 打车距离与打车费用数据表

现在，问一个问题，假设有个乘客坐出租车行驶 20 公里，请问应该支付多少费用？
抛开机器学习的知识，或者说暂时先忘记，我们用自己的思维方式来解决问题，大部分人会按照如下思路解决问题：

我们会从现有数据中找到打车距离与费用之间的规律：

• 先假定，再验证是否正确。
• 正确，执行下一步；错误，重复上一步再假定。

具体我们定义如式8这样的函数：
$$
y = w \cdot x+b
$$

式8

其中$y$表示打车费用，$w$表示每公里费用，$x$表示打车距离，$b$表示起步价，这里我们先假设$w = 1$，$b = 1$，根据函数计算出打车费用，如表9：

距离（公里）	实际费用（元）	预计费用（元）
1	15	2
2	18	3
3	21	4
4	24	5
5	27	6
6	30	7
7	33	8
8	36	9
9	39	10
10	42	11
11	45	12
12	48	13
13	51	14
14	54	15
15	57	16

表9

显然，经过通过表格中数据的对比，发现我们假设的$w$和$b$不正确，因为预计费用与实际费用相差太大了，所以我们需要重新假设，直到预计费用与实际的费用近似为止。最后使用这个函数去计算出20公里的打车费用。这是也是大部分人的思维方式。

但是要想机器学习思路跟我们自己的思维方式一样的话，就要引出新的问题了：

1. 怎么验证正确？有没有一个评判标准，用来评价我们假定的规律是正确的或者说是近似的。
2. 怎么趋近正确？当知道不确定之后，如何让假定的规律趋近正确。

针对上面这个两个问题，这就需要用到下面讲的损失函数与梯度下降。

损失函数

损失函数（Loss Function）用于衡量模型的预测结果与实际观测值之间的差异。损失函数在某些地方又称为：代价函数、目标函数、误差函数、成本函数、偏差函数。

损失函数是优化算法的基础，通过最小化损失函数，我们可以得到更准确的模型参数。拿上面打车需求来说，就是得到通过最小化损失函数从而得到更准确的$w$和$b$，以用来解决上一节“怎么验证正确”这个问题。

损失函数有很多种，常见的有：平均绝对误差，均方误差，交叉熵等等，接下来给大家介绍几种常见的损失函数。

平均绝对误差损失函数（Mean Absolute Error, MAE）

$$
MAE = \frac{1}{n}\sum^{n}_{i=1}|\hat{y}_i-y_i|
$$

式10 平均绝对误差

其中$n$表示样本数量，$i$表示第几个样本，$\hat{y}_i$表示预测值，$y_i$表示实际值，如图11所示，横坐标是预测值与实际值差值，纵坐标是损失函数值：

图11 平均绝对误差函数图

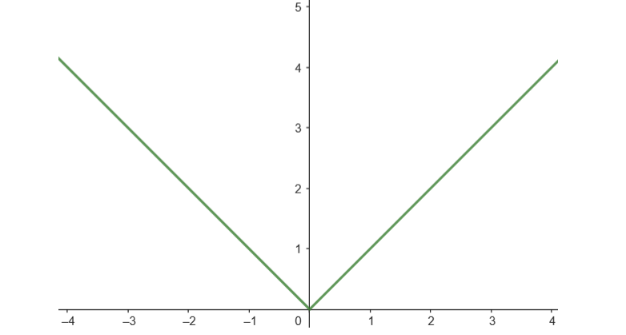
当所有样本的预测值与实际值差异较小时，MAE值较小，这表示模型的预测结果越准确。当所有样本的预测值与实际值差异较大时，MAE值较大，这表示模型的预测结果越不准确。

均方误差损失函数（Mean Squared Error, MSE）

$$
MSE = \frac{1}{n}\sum^{n}_{i=1}(\hat{y}_i-y_i)^2
$$

式12 均方误差损失函数

其中$n$表示样本数量，$i$表示第几个样本，$\hat{y}_i$表示预测值，$y_i$表示实际值，如图13所示:

图13 均方误差损失函数图

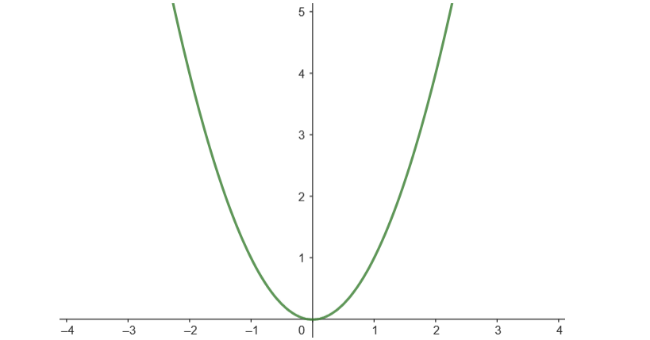
当所有样本的预测值与实际值差异较小时，MSE值较小，这表示模型的预测结果越准确。当所有样本的预测值与实际值差异较大时，MSE值较大，这表示模型的预测结果越不准确。

关于熵的概念以及交叉熵损失：

在理解交叉熵损失函数之前，我们需要先了解一下关于熵的概念。

熵（Entropy）：

熵是一个在不同领域（包括热力学、信息理论和统计学）中具有不同含义的概念。在热力学中，熵是系统的无序度或混乱度的度量，通常与热能传递和能量分布有关。在信息理论中，熵是信息的度量，表示信息的不确定性或信息量。熵越高，信息越不确定，熵越低，信息越确定。信息熵通常使用对数底为2的对数，以比特（bits）为单位来表示。

信息熵（Shannon Entropy）：

信息熵是信息理论中的一个概念，由香农（Claude Shannon）提出。它用于度量一组数据或随机变量的不确定性或信息量。信息熵的公式如下：
$$
H(X) = -\sum_{i} p(x_i) \log_2(p(x_i))
$$

式14 信息熵公式

其中，$H(X)$ 表示随机变量 $X$ 的信息熵，$p(x_i)$ 是随机变量 $X$ 取得值 $x_i$ 的概率。信息熵的值衡量了随机变量的不确定性。当所有可能的值都具有相等的概率时，信息熵最大。当某些值的概率较高而其他值的概率较低时，信息熵较低。

举个例子，判断一个西瓜是否好瓜的不确定性：

在这个示例中，我们将使用信息熵来衡量关于西瓜是否是好瓜的不确定性。

假设有一堆西瓜，我们随便挑选其中一个出来，分辨出是“好瓜”（好吃的）或“坏瓜”（不好吃的）怎么分辩呢? 我们可以通过瓜的颜色、波纹、瓜柄、大小等特征综合进行判断。

为了简化例子，本例子暂时不使用任何特征进行判断，仅仅通过历史数据来判断概率，为了计算这些样本的好瓜/坏瓜标签的不确定性，可以使用信息熵。

首先，我们需要知道每种标签（好瓜或坏瓜）在数据集中的概率。假设有10个样本中有6个是好瓜，4个是坏瓜，那么好瓜的概率是0.6，坏瓜的概率是0.4。

然后，我们可以使用信息熵的公式来计算不确定性：

在这个例子中，$X$ 表示好瓜或坏瓜标签。

• 对于好瓜（好吃的），信息熵为：
  $$
  H(\text{“好瓜”}) = -[0.6 \cdot \log_2(0.6) + 0.4 \cdot \log_2(0.4)]=0.9709516
  $$

• 对于坏瓜（不好吃的），信息熵为：
  $$
  H(\text{“坏瓜”}) = -[0.6 \cdot \log_2(0.6) + 0.4 \cdot \log_2(0.4)]=0.9709516
  $$

现在，我们可以计算好瓜和坏瓜的信息熵，以衡量关于西瓜是否是好瓜的不确定性。如果信息熵较高，表示我们对于是否是好瓜的判断较不确定；如果信息熵较低，表示我们对于是否是好瓜的判断较确定。

交叉熵（Cross-Entropy）

交叉熵，交叉熵是信息论中的一个重要概念，主要用于度量两个概率分布间的差异性。
$$
H(p,q)=-\frac{1}{n}\sum^{n}_{i=1}p(x_i)\log_2(q(x_i))
$$

式15 交叉熵损失函数

$p(x)$表示样本的真实分布，$q(x)$表示模型所预测的分布。

交叉熵是一种用于衡量两个概率分布之间差异的指标。在机器学习中，这通常表示了模型的预测概率分布与实际或真实概率分布之间的差异。当交叉熵的值越小时，意味着模型的预测概率分布与真实概率分布越接近，模型的预测效果越好。因为交叉熵是一种损失函数，通常在模型训练中用来衡量模型的性能，所以越小的交叉熵值表示模型的性能越好。

交叉熵损失函数（Cross-Entropy Loss Function）

交叉熵在分类问题中常常与softmax是标配，softmax将输出的结果进行处理，使其多个分类的预测值的和为1，再通过交叉熵损失函数来计算损失。

$$
L(y,\hat{y}) = -\frac{1}{n}\sum^{n}_{i=1}[y_i \cdot \log{\hat{y}}+(1-y_i) \cdot \log{(1-\hat{y})}]
$$

式16 交叉熵损失函数

其中$n$表示样本数量，$i$表示第几个样本，$\hat{y}$表示预测值， $y_i$表示实际值，其中$log$表示自然对数，以自然常数$e$为底数，不是10为底数。上面公式可以拆开成两部分：一种情况当$y = 1$时，即实际值为1，另外一种情况当$y = 0$时，即实际值为0，如图17所示：

图17 交叉熵损失函数图

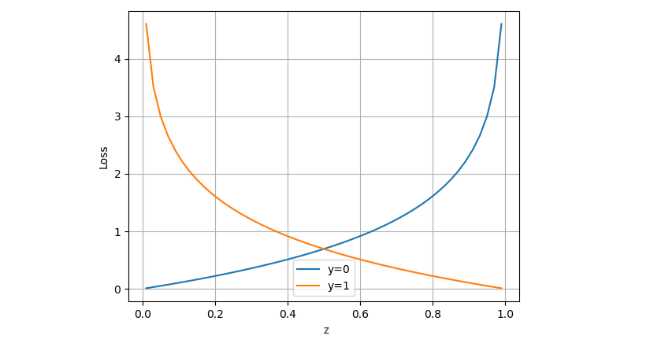
横坐标是预测输出（通常表示为 $\hat{y}$），纵坐标是损失函数值。当 $y=1$ 时，表示当前样本的实际值是正类。此时，损失函数的值越小，结果越准确，即当预测输出 $\hat{y}$ 越接近1时，损失函数值越小，表明模型的预测越准确。当 $y=0$ 时，表示当前样本的实际值是负类。同样，此时，损失函数的值越小，结果越准确，即当预测输出 $\hat{y}$ 越接近0时，损失函数值越小，表明模型的预测越准确。当预测输出 $\hat{y}$ 偏离了实际类别（无论是正类还是负类）时，对应项的损失函数值会增加，从而表明模型的预测不准确。这就是交叉熵损失函数的目标：通过最小化损失函数值来推动模型的预测尽量接近实际标签。

交叉熵的具体例子，我们可以考虑二分类问题，其中我们试图预测某个事件是否发生。在这个情景下，交叉熵通常被用来衡量模型的性能。

假设我们有一个二分类问题，其中我们要预测一封电子邮件是否是垃圾邮件。对于每一封电子邮件，我们有以下情况：

• 实际标签 $y$：1 表示垃圾邮件，0 表示非垃圾邮件。
• 模型的预测 $\hat{y}$：模型根据邮件的特征进行预测，输出一个概率值，表示该邮件为垃圾邮件的概率。

现在，我们可以使用交叉熵来衡量模型的性能。交叉熵损失函数的表达式如下：

$$
Loss = -[y \cdot \log{\hat{y}} + (1 - y) \cdot \log{(1 - \hat{y})}]
$$

现在，让我们考虑一些情况：

情况一： 如果一封电子邮件是垃圾邮件（$y=1$），而模型的预测 $\hat{y}$ 接近1，表示模型正确地将其识别为垃圾邮件。在这种情况下，交叉熵损失会趋近于0，因为第一项 $y \cdot \log{\hat{y}}$ 的值接近0。

情况二： 如果一封电子邮件是垃圾邮件（$y=1$），但模型的预测 $\hat{y}$ 接近0，表示模型错误地将其识别为非垃圾邮件。在这种情况下，交叉熵损失会增加，因为第一项 $y \cdot \log{\hat{y}}$ 的值会增大。

情况三： 如果一封电子邮件不是垃圾邮件（$y=0$），而模型的预测 $\hat{y}$ 接近0，表示模型正确地将其识别为非垃圾邮件。在这种情况下，交叉熵损失会趋近于0，因为第二项 $(1 - y) \cdot \log{(1 - \hat{y})}$ 的值接近0。

情况四： 如果一封电子邮件不是垃圾邮件（$y=0$），但模型的预测 $\hat{y}$ 接近1，表示模型错误地将其识别为垃圾邮件。在这种情况下，交叉熵损失会增加，因为第二项 $(1 - y) \cdot \log{(1 - \hat{y})}$ 的值会增大。

通过计算所有样本的交叉熵损失，并对其求平均，可以评估模型的性能。总体而言，交叉熵损失越小，表示模型的分类预测越准确。

梯度下降

上一节我们已经通过损失函数解决了“怎么验证正确”这个问题。但是还有一个问题“怎么趋近正确”，这个问题的解决方法就是我们接下来要讲解的梯度下降。

梯度下降（Gradient Descent）是一种常用的优化算法，用于最小化损失函数。它是机器学习中最基础的优化算法之一，用于更新模型参数以使成本函数达到最小值。梯度下降的核心思想是通过计算成本函数关于模型参数的梯度（导数），沿着梯度的反方向更新参数，使成本函数逐步减小，最终收敛到局部最优解或全局最优解。

为了大家更好理解，举个寻找山谷最低点的例子。想象一下，你被放在一个充满高低不平的山地中，目标是找到最低点以安营扎寨。现在的问题是，你被蒙上了眼睛，不能直接看到哪里是最低点。

1. 初始位置（初始化参数）：首先，你需要一个起点，这在梯度下降中就相当于初始化参数。也就是说，你一开始站在山上的某个地方。
2. 感受坡度（计算梯度）：因为你的眼睛被蒙住了，你只能通过脚下的坡度来感觉哪里可能是下坡。在梯度下降中，这个“感觉”就是通过计算损失函数的梯度来实现的。
3. 小心翼翼地迈一步（更新参数）：感受到坡度后，你会朝着下坡最陡的方向迈出一步。在梯度下降中，这一步对应于用当前点的梯度来更新模型参数。
4. 步长的选择（学习率）：你得决定这一步要走多远。走得太远，可能会错过最低点或者走到另一个山坡上去；走得太短，下山的速度就会很慢。在梯度下降中，这个“多远”通常由学习率来控制。
5. 循环迭代（多次更新参数）：一步一步地，你继续朝着感觉到的下坡方向前进，直到觉得已经不能再下去了（即梯度接近或等于零），或者觉得已经走够多的步数了。
6. 到达目的地（收敛）：最终，你会觉得自己到达了一个相对较低的地方，那么恭喜你，你的下山冒险就此完成。在梯度下降中，这意味着算法找到了一个损失函数的最小值。

通过这样的下山过程，如图18所示：

图18 下山过程

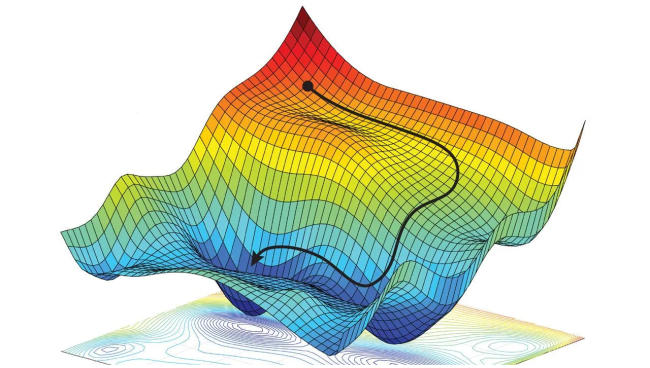
梯度用来控制下山的方向，学习率用来控制下山的步长或者说速度。总之，梯度下降算法是在不断地“摸索”和“尝试”，最终找到一个能让损失函数达到最小值的模型参数解。

上面是从下山过程给大家整体描述，但肯定还有人不理解梯度如何影响到下山方向的。接下来我们使用代码配合函数图给大家详细阐述。我们还是拿打车需求来说明，但为了计算方便，也为了大家好理解，这里我们假定打车的数据只有一条，并且假定b=12 是固定不变的，我们可以使用代码计算各种代码计算出各种假定w的均方误差值，代码如下：

# 实际打车费用
y_true = 15

# 计算打车费用，x 打车距离，w 每公里费用，b 起步价
def calc(x, w, b):
    return x * w + b

# 计算均方误差
def mean_squared_error_np(y_true, y_pred):
    return (y_pred - y_true)**2

# 假定 w = 1，b = 12，计算打车费用，此时均方误差为 4
print("MSE:", mean_squared_error_np(y_true, calc(1, 1, 12))) 

# 假定 w = 3，b = 12，计算打车费用，此时均方误差为 0
print("MSE:", mean_squared_error_np(y_true, calc(1, 3, 12))) 

# 假定 w = 5，b = 12，计算打车费用，此时均方误差为 4
print("MSE:", mean_squared_error_np(y_true, calc(1, 5, 12)))

依照上面计算结果，我们可以画出如图19所示：

图19 损失函数

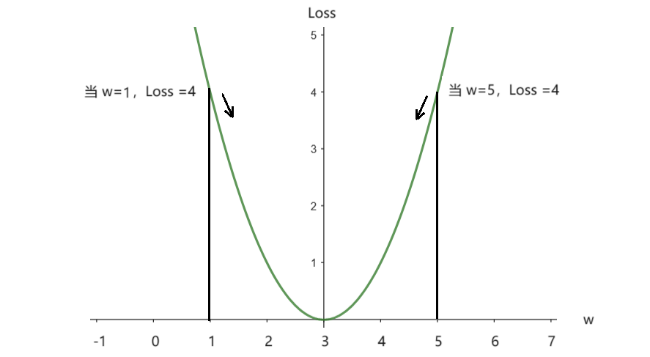
无论$w=1$还是$w=5$时，我们都希望想要Loss值变少，朝着函数底部迈进，这样我们假定的函数才是越准确的，那么想要函数向底部迈进，就要让$w$趋近于 3，意味着，当$w=1$时，就让要$w$变大，当$w=5$时，就要让$w$变小。

那我们怎么才知道现在w到底是大还是小呢，或者说能不能用一个统一的方法搞定呢？答案是可以的，利用损失函数的梯度就可以搞定，但这里涉及到微积分求导，若有同学对为微积分求偏导数不清楚参考书籍后面的附录。上面的损失函数，其数学公式如式20：
$$
Loss=(w \cdot x + 12 -y)^2
$$

式20 损失函数

其中$w$表示每公里费用，$x$表示打车距离，$y$表示实际打车费用。我们利用微积分求偏导数计算出该函数的梯度如式21：
$$
\frac{δLoss}{δw}=2 \times (w\times x + 12 -y) \times x
$$

式21 求梯度

现在分别代入各个参数值，计算出当$w = 1$时，梯度为-4，表示$w$小了；当$w=5$时梯度为4，表示w大了。如图22所示：

图22 损失函数梯度

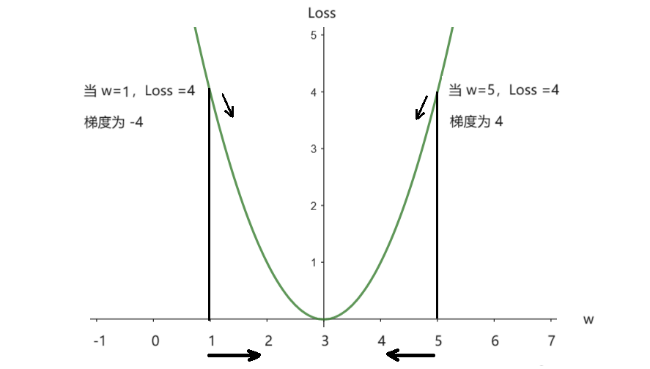
我们就可以利用下面公式对w进行更新的调整：
$$
w = w - a \times \frac{δLoss}{δw}
$$

式23 对权重更新

其中，$a$表示学习率，用来控制更新步长的或者说着更新速度的。到此，通过上面的讲解，证明了梯度可以用来控制$w$更新的方向，让损失函数往最优解收敛。

学习率

学习率（Learning Rate），是一个非常重要的超参数，用于控制模型在优化过程中参数更新的幅度。具体来说，当我们使用梯度下降或其相关算法进行优化时，学习率决定了每一步沿着负梯度方向走多远。

但要注意的是：如果学习率太大，模型可能在最小值附近震荡，甚至可能导致模型发散，从而无法收敛。如果学习率太小，模型收敛得非常慢，需要更多的迭代次数，这会增加计算成本。如图24所示：

图24 学习率过大或过小图

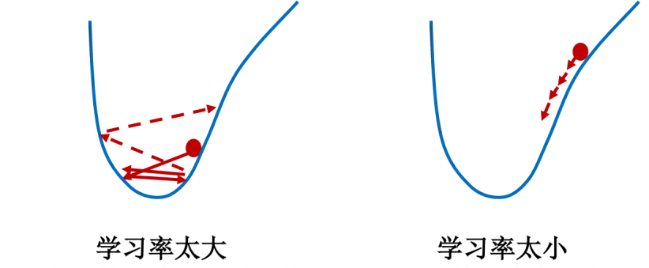
所以一个合适的学习率可以使模型在合理的时间内收敛到一个相对不错的解。

基础案例应用

上一节我们把损失函数与梯度下降讲解完，知道如何评价结果是否正确以及如何趋近正确的结果。接下来，我们用代码演示机器学习中两个案列，加深大家对机器学习的理解。在写代码前，这里说明机器学习的一般步骤：

1. 收集数据：因为数据的数量和质量直接决定了预测模型的好坏。
2. 数据处理：一般会划分训练集和测试集，目的主要是为了评估模型的泛化能力，也就是模型对未见过的新数的预测能力。
3. 选择一个算法（或模型）：不同算法适合解决不同问题，打车需求我们选择线性回归模型，学生录取预测我们选择逻辑回归模型。
4. 训练：通过数据喂给模型，让其找到规律，即找到合适的参数，达到损失函数的最优解的过程。
5. 评估：一旦训练完成，就可以评估模型是否有用。
6. 参数调整：如果评估发现模型不好，那么就需要调整参数，这里值的是超参数，比如学习率等。
7. 预测：如果评估发现模型好，那么利用模型来解决我们的问题。

案例一、使用线性模型预测打车费用

下面仅用numpy来实现一个打车费用预计的机器学习模型，如代码25所示：

import numpy as np

def load_data():
  # 数据
  data = np.array([
    [1.0, 15.0], [2.0, 18.0],
    [3.0, 21.0], [4.0, 24.0],
    [5.0, 27.0], [6.0, 30.0],
    [7.0, 33.0], [8.0, 36.0],
    [9.0, 39.0], [10.0, 42.0],
    [11.0, 45.0], [12.0, 48.0],
    [13.0, 51.0], [14.0, 54.0],
    [15.0, 57.0]
  ])
  # 划分数据集，分训练集和测试集
  ratio = 0.8
  offset = int(data.shape[0] * ratio)
  train_data = data[:offset]
  test_data =  data[offset:]
  x_train_data = train_data[:, 0:1]
  y_train_data = train_data[:, 1:2]
  x_test_data = test_data[:, 0:1]
  y_test_data = test_data[:, 1:2]
  return x_train_data, y_train_data, x_test_data, y_test_data

class MyNet:
    # 初始 w 和 b
    def __init__(self, w, b):
        self.w = w
        self.b = b
        
    # 计算预测值
    def foward(self, x):
        z = np.dot(self.w, x) + self.b
        return z

    # 计算成本
    def loss(self, y, z):
      error = z - y
      return np.mean(error * error)

    # 计算梯度
    def gradient(self, x, y, z):
      dw = np.mean((z - y) * x)
      db = np.mean(z - y)
      return dw, db

    # 更新 w 和 b
    def update(self, dw, db, learning_rate):
      self.w = self.w - learning_rate * dw
      self.b = self.b - learning_rate * db

    # 训练
    def train(self, x, y, learning_rate = 0.01):
      for i in range(1, 5001):
        # 计算预测值
        z = self.foward(x)
        # 计算成本
        loss = self.loss(y, z)
        # 计算梯度
        dw, db = self.gradient(x, y, z)
        # 更新参数
        self.update(dw, db, learning_rate)

        if(i % 1000 == 0):
          print('第{}次预测值:'.format(i), z)
          print('第{}次成本值:'.format(i), loss)
          print('第{}次梯度值:'.format(i), dw, db)
          print('第{}次w和b的值:'.format(i), self.w, self.b)

# 获取数据
x_train_data, y_train_data, x_test_data, y_test_data = load_data()

# 创建模型对象
myNet = MyNet(1, 1)

# 训练
myNet.train(x_train_data, y_train_data)

# 预测测试数据
z = myNet.foward(x_test_data)
print('测试数据的预测值：', z)

# 评估测试数据
loss = myNet.loss(y_test_data, z)
print('测试数据的成本值：', loss)

# 预测 20 公里打车费用
print('20 公里打车费用：', myNet.foward(np.array([20])))

代码25 打车费用预测模型代码

案例二、使用逻辑回归预测学生录取

先说明以下预测学生录取，其需求是根据学生两门考试成绩来对应学生能否录取进行预测。如代码26所示：

import numpy as np

# 读取数据
data = np.array([
    [45.6, 80.1, 1],
    [32.5, 60.0, 0],
    [52.0, 75.5, 1],
    [28.6, 45.2, 0],
    [60.1, 85.3, 1],
    [47.2, 49.5, 0],
    [65.4, 90.1, 1],
    [35.6, 40.8, 0],
    [55.8, 77.4, 1],
    [38.1, 52.5, 0],
    [72.5, 95.0, 1],
    [25.1, 30.5, 0],
    [64.2, 82.7, 1],
    [40.0, 45.6, 0],
    [70.5, 92.2, 1]
])
x = data[:, :-1]
y = data[:, -1]

# 数据集分割（训练集和测试集）
train_size = int(0.8 * len(data))
x_train, x_test = x[:train_size], x[train_size:]
y_train, y_test = y[:train_size], y[train_size:]

# 初始化权重和偏置项
w = np.zeros(x.shape[1])
b = 0.0

# Sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 交叉熵损失函数
def loss(y, y_pred):
    epsilon = 1e-15
    y_pred = np.clip(y_pred, epsilon, 1 - epsilon)
    return -np.mean(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred))

# 学习率
learning_rate = 0.01
# 迭代次数
epochs = 1001

for epoch in range(1, epochs):
    z = np.dot(x_train, w) + b
    y_pred = sigmoid(z)
    gradient_w = np.dot(x_train.T, y_pred - y_train) / train_size
    gradient_b = np.sum(y_pred - y_train) / train_size
    w -= learning_rate * gradient_w
    b -= learning_rate * gradient_b
    if epoch % 100 == 0:
        train_loss = loss(y_train, y_pred)
        print(f'Epoch {epoch}: Loss {train_loss}')

# 预测函数
def predict(x):
    return np.round(sigmoid(np.dot(x, w)))

# 测试模型
y_test_pred = predict(x_test)
test_loss = loss(y_test, sigmoid(np.dot(x_test, w) + b))
accuracy = np.mean(y_test_pred == y_test)
print(f'Final Test Loss: {test_loss}')
print(f'Accuracy: {accuracy * 100:.2f}%')

代码26 预测学习是否能录取代码

神经网络基础

神经网络是一种模拟人脑工作机制的算法。最简单的神经网络（感知机、单层网络等）在数十年前就已经出现。深度学习就是应用了多层（通常很多层）神经网络进行学习的一种特殊形式。那为什么要使用深度学习呢？原因如下：

1. 数据复杂性：在有大量数据和复杂的数据结构的情况下，浅层网络往往难以捕捉数据背后的复杂关系。深度网络能自动地从原始数据中学习有用的特征。
2. 自动特征工程：传统的机器学习方法依赖于人工提取的特征。而深度学习能自动进行“特征工程”，这极大地减少了人工干预的需要。
3. 通用性：经过适当的训练和调整，同一个深度学习模型往往可以适用于多种不同的任务。
4. 高准确率：在图像识别、自然语言处理、强化学习等领域，深度学习模型已经达到或超过了人类的性能。
5. 硬件发展：现代硬件（尤其是 GPU）的发展使得更大、更复杂的神经网络成为可能，这也推动了深度学习的应用。
6. 大数据时代：随着数据量的爆炸性增长，深度学习模型（需要大量数据才能表现得更好）自然而然地变得更有吸引力。

总而言之，神经网络为深度学习提供了基础框架，而深度学习则是这个基础之上的一种更高级、更复杂的实现，它能更好地处理大规模和高复杂度的数据。

生物神经元

人脑可以看作是一个生物神经网络，由众多的神经元连接而成。各个神经元传递复杂的电信号，树突接收到输入信号，然后对信号进行处理，通过轴突输出信号。如图27所示：

图27 生物神经元示意图

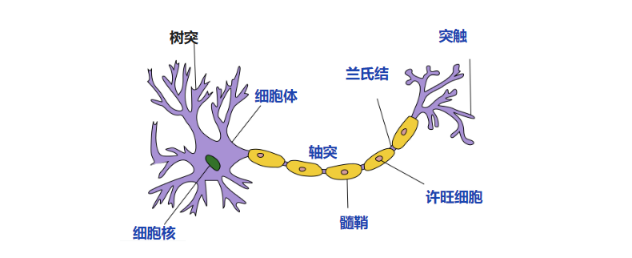
神经细胞结构大致可分为：树突、突触、细胞体及轴突。单个神经细胞可被视为一种只有两种状态的机器，激活时为“是”，而未激活时为“否”。神经细胞的状态取决于从其它的神经细胞收到的输入信号量，及突触的强度（抑制或加强）。当信号量总和超过了某个阈值时，细胞体就会激动，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。

人脑由大约860亿个神经元（neurons）以及大约1万亿个突触（synapses，神经元之间的连接）组成。这些神经元和突触构成了一种极为复杂的网络，负责处理和存储信息。

感知机

感知机（perceptron）是一种人工神经元，是生物神经元的简单抽象。感知机由科学家弗兰克·罗森布拉特（Frank Rosenblatt）发明于1950至1960年代，他受到了来自沃伦·麦卡洛克（Warren McCulloch）和沃尔特·皮茨（Walter Pitts）的更早工作的启发。

为了模拟神经细胞行为，与之对应的感知机基础概念被提出，权量（突触）、偏置（阈值）及激活函数（细胞体）。

感知机是怎么工作的呢？感知机的输入是几个二进制，输出是一位单独的二进制，如图28所示：

图28 感知机

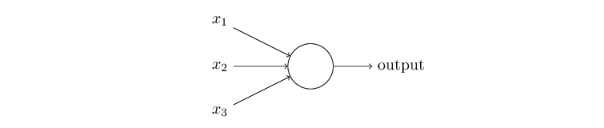
本例中的感知机有三个输入: $x_1$,$x_2$,$x_3$。通常，它可以有更多或者更少的输入。罗森布拉特提出了一种计算输出的简单的规则。他引入了权重（weight）: $w_1$,$w_2$,$w_3$，等实数来表示各个输入对于输出的重要程度。神经元的输出是 0 还是 1，由加权和是否小于或者大于某一个阈值（threshold value）。和权重一样，阈值也是一个实数，同时它是神经元的一个参数。使用更严密数学公式来表示如式29：

式29 加阈值

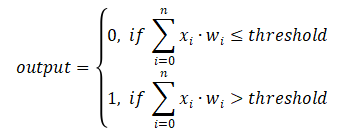
这就是感知机的工作方式！通过调整权重和阈值的大小，我们可以得到不同的决策模型。也可以通过多层感知机，实现更复杂的决策，如图2-13所示：

图30 多层感知机

比如我可以使用多层感知机解决异或问题，异或的运算方法：真⊕假=真、假⊕真=真、假⊕假=假、真⊕真=假，如图31所示：

图30 感知机解决异或问题

这样我们的感知机就可以胜任所有的数学运算，因为所有数学运算都是由最基本运算AND、OR、NAND、XOR构成。

感知机的计算普遍性既让人感到安心，也让人感到失望。说它是安心的，因为感知机网络与任何其它的计算设备拥有同样强大的计算能力。说它是令人沮丧的，很多东西也具备这个能力。

不过，情况还是相对比较乐观的。我们可以设计学习算法（learning algorithm）使得能够自动地调整人工神经元网络的权重和偏置。这种调整能够对外部刺激做出响应，而不需要程序员的直接干预。这些学习算法使得我们能够用一种与传统逻辑门从根本上不同的方法使用人工神经元。

激活函数及其作用

当神经网络中的每个神经元只进行线性变换（例如简单的加权和求和）时，多个线性变换的组合仍然只能表示线性关系。这限制了神经网络的表示能力，使其无法处理更复杂的非线性关系和模式。

激活函数通过对神经元的输出进行非线性变换，将线性组合的结果映射到非线性空间中。这使得神经网络能够学习和表示更复杂、非线性的模式和关系。激活函数引入了非线性性质，使得神经网络能够逼近任意复杂度的函数。

下面给大家阐释激活函数是如何给感知机引入非线性的。我们现在有只有一个输入的神经元，为引入激活函数，其函数如式31所示：
$$
y=w \cdot x +b
$$

式31 线性函数

无论我们如何修改w和b两个的值，其函数都是线性的，如图32所示：

图32 函数都呈现线性

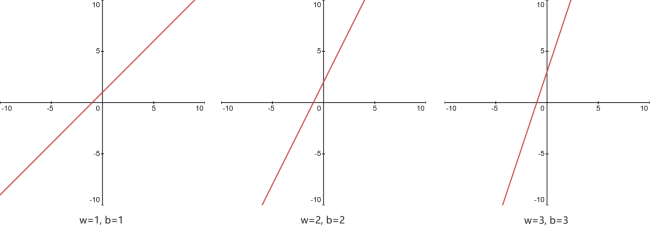
若引入Sigmoid激活函数对上面函数进行处理，其函数如式33所示：
$$
y=\frac{1}{1+e^{-(w \times x+b)}}
$$

式33 sigmoid激活函数

同样地，我们修改w和b两个的值，函数就变成了非线性的，如图34所示：

图34 函数都呈现非线性

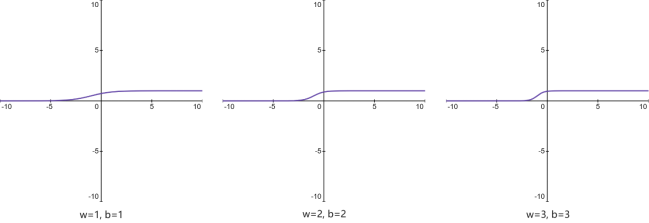
如果我们把w改得特别大，比如1000，之后我们分别试下当$b=10$，$b=50$，$b=100$的情况，如图35所示：

图35 类似阶跃函数

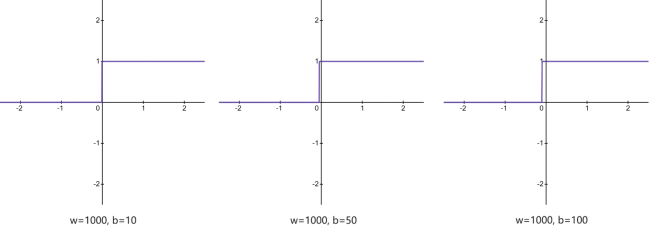
我们发现$w$值越大，曲线部分越陡，而阶跃位置是 $-b \div w$计算出的值。

加入激活函数不仅可以引入非线性，也可以让神经网络能够逼近任意复杂度的函数，比如我们想让神经网络拟合一个山峰状一样的函数，那我们设计一个神经网络，接收一个输入，如图36所示：

图36 由三个神经元构成的神经网络

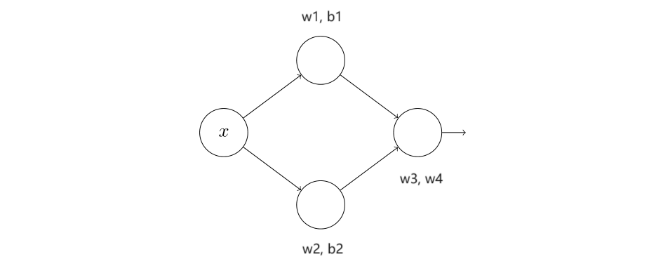
这样的神经网络意味着我们可以调整的参数有6个，$w_1$，$w_2$，$w_3$，$w_4$，$b_1$，$b_2$，最后一个神经元不使用激活函数，也没有偏置，那么神经网络的输出如式37所示：
$$
y=\frac{1}{1+e^{-(w_1 \times x + b_1)}} \times w_3 + \frac{1}{1+e^{-(w_2 \times x + b_2)}} \times w_4
$$

式37

如果我们分别对参数设置成：$w_1=100$，$w_2=100$，$w_3=0.8$，$w_4=0.8$，$b_1=-10$，$b_2=-60$，那么神经网络的函数就会长成这样，如图39所示：

图39 山峰状的函数

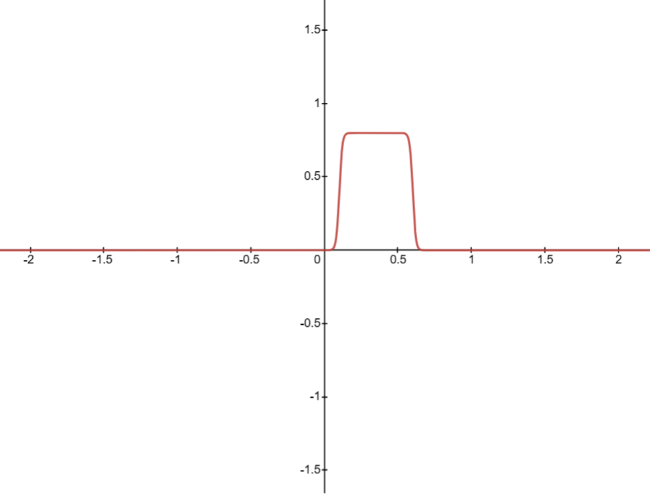
这里仅仅是让神经网络拟合山峰状的函数，其还可以拟合更复杂的函数，只要加入更多的神经元和设置合理的参数值即可。到此我们就把激活函数的作用讲完了。

全连接神经网络

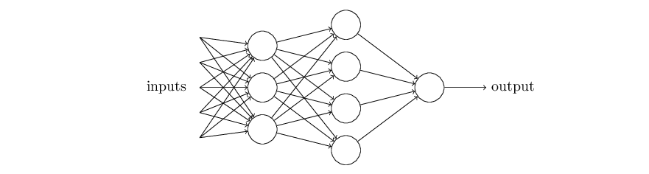
全连接神经网络（Fully Connected Neural Network，也称为多层感知机 Multilayer Perceptron, MLP）是一种最基础和最简单的神经网络架构。在这种网络中，每一层的所有神经元都与前一层和后一层的所有神经元相连接，如图40所示：

图40 全连接神经网络

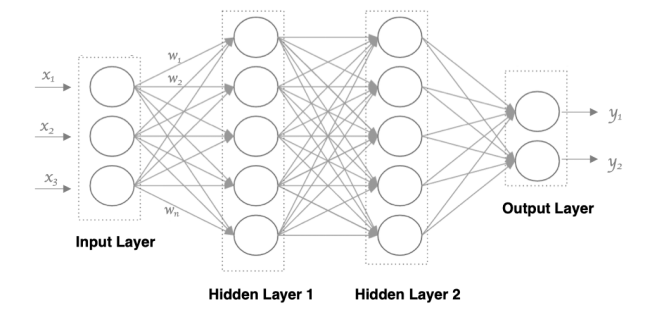
全连接神经网络基本组成：

1. 输入层（Input Layer）：接收输入数据，通常与特征的数量相匹配。
2. 隐藏层（Hidden Layers）：一个或多个层，每层包含任意数量的神经元。这些层通过激活函数引入非线性。
3. 输出层（Output Layer）：生成预测或分类结果。输出层的神经元数量通常与任务的需求相匹配（例如，二分类问题通常有一个输出神经元，多分类问题则有多个）。

全连接神经网络特点：

1. 灵活性：全连接神经网络可以拟合非常复杂的函数。
2. 参数多：由于每一层都是全连接的，因此参数数量可能会很大，导致过拟合。
3. 计算密集：大量的连接和参数意味着需要更多的计算资源。
4. 局限性：全连接神经网络不具备局部感知和平移不变性，这在一些任务（如图像识别）中是不利的。

全连接神经网络运算过程：

1. 前向传播（Forward Propagation）：输入数据通过每一层的权重和激活函数，从输入层传递到输出层。
2. 损失计算（Loss Calculation）：在输出层，模型的预测与实际标签进行比较，计算损失。
3. 反向传播（Backpropagation）：计算损失函数关于每个权重的梯度，并更新权重。
4. 优化（Optimization）：使用梯度下降或其他优化算法来最小化损失函数。

全连接神经网络应用包括分类问题（如垃圾邮件检测、图像分类），回归问题（如房价预测），推荐系统等。虽然复杂任务通常使用更为高级的网络结构，如卷积神经网络（CNN）、循环神经网络（RNN）和Transformer等，但是全连接神经网络是神经网络研究和应用的基础，只有学好这个才能为后面更复杂网络结构的学习打下良好的基础。

使用全连接网络预测打车费用

如果我们自己使用代码来搭建神经网络，会涉及到大量数学运算，所以我们框架来提升我们的开发效率，这里我们选用的框架是百度飞桨，建议大家使用AI Studio 中编写代码，如代码41所示：

# 导入对应的依赖模块
import numpy as np
import paddle

# 定义数据集的封装, 主要包括特征值和目标值
# 特征值: 需要输入的每一个指标, 目标值: 对应的是输出结果
class MyDataset(paddle.io.Dataset):
    def __init__(self, data):
        super().__init__()
        # 构造函数初始化
        self.data = data
    # 魔法方法, 
    def __getitem__(self, index):
        # 对于获取的一个数据进行解包, x: 特征值  y:目标值
        x, y = self.data[index]
        
        # 返回指定类型的数据, 把x维度提升为二维数组  y提升为为二维数组
        return np.array(x, dtype='float32'), np.array(y, dtype='float32')
    
    # 魔法方法, 获取对应的数据集的长度
    def __len__(self):
        return len(self.data)
        
# 张量与numpy的数组是类似概念
 
# 设置对应的数据集
x_data = paddle.to_tensor([[1.], [3.0], [5.0], [9.0], [10.0], [20.0]])

# 设置对应的目标集
y_data = paddle.to_tensor([[12.], [16.0], [20.0], [28.0], [30.0], [50.0]])

#zip 方法把对应的x,y 封装为一个元组对象的列表对象
data = list(zip(x_data, y_data))
dataset = MyDataset(data)

# 创建一个线性模型 y=wx+b
linear =  paddle.nn.Linear(1, 1)

# 对模型进行组网 构建一个顺序执行的神经网络的容器
mynet = paddle.nn.Sequential(linear)

# 创建对应的模型
model = paddle.Model(mynet)

# optimizer 设置优化器: 使用的是Adam 优化, 其中learning_rate学习率  parameters: 模型的参数
# loss:paddle.nn.MSELoss() 均方误差的损失
model.prepare(optimizer=paddle.optimizer.Adam(learning_rate=0.001,parameters=model.parameters()),loss=paddle.nn.MSELoss())

# 开始训练模型, 设置数据集, batch_size: 每次训练多少个样本, epochs: 循环的次数, verbose=1: 显示日志信息
model.fit(dataset, batch_size=64, epochs=10, verbose=1)

# 学习过后的一个参数
w_after_opt = linear.weight.numpy().item()
b_after_opt = linear.bias.numpy().item()

print("w after optimize: {}".format(w_after_opt))
print("b after optimize: {}".format(b_after_opt))

代码41 全连接神经网络实现打车费用预测

注意：这里仅仅是通过这个代码给大家演示如何使用百度飞桨的 API 搭建神经网络，并为后面的章节的讲解做铺垫，实际上大家会发现其准确率并没有我们之前所编写的代码高，那是因为预测打车费用的需求并不复杂，并不适合用神经网络，即使要用，也只需要用一个神经元即可。换句话说，要解决的问题越复杂，神经网络层数与神经元数量会越多；反之，神经网络层数与神经元数量会越少。

原理剖析：前向传播与反向传播

到此大家肯定有疑问，为何神经网络能学习到合适的参数（包含权重和偏置）的呢？这里就涉及神经网络的前向传播，损失计算，反向传播，参数更新等。接下来我为大家逐个讲解，但在讲解之前，为了大家更好的理解，我们会适当做一些简化。

前向传播

神经网络的前向计算是指将输入数据传递通过网络中的各层以获得最终的输出，如图42所示：

图42 神经网络前向计算

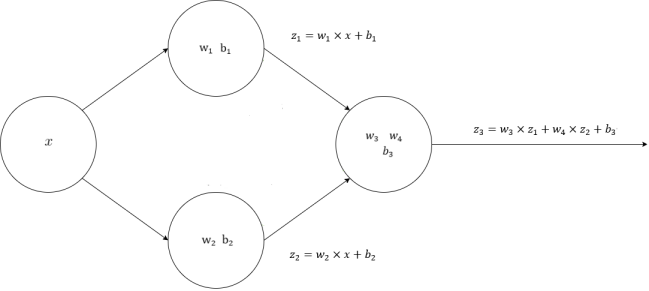
这个过程包括以下步骤：

初始化权重和偏差：在进行前向计算之前，你需要初始化神经网络中每个神经元的权重和偏差。这些参数决定了神经元如何对输入数据进行加权和偏移，从而生成输出。拿我们的神经网络来说，输入一条数据 [1.0, 15.0] 为例：
$$
x=1.0, y=15.0
$$
上面的神经网络合计总共4个权重，3个偏置，如下进行初始化，即假定一个值，如下：
$$
w_1=0.1 , w_2=0.2 , w_3=0.3 , w_4=0.4 , b_1=0.1 , b_2=0.2 , b_3=0.3
$$
输入层：将输入数据传递到神经网络的输入层。输入层通常不对输入数据进行任何处理，只是将数据传递到下一层。

隐藏层：将输入数据从输入层传递到隐藏层（可能有多个隐藏层）。在每个隐藏层中，每个神经元将输入加权求和，并应用一个激活函数来生成激活值。这个值则成为下一层的输入。拿我们的神经网络来说，隐藏层有两个神经元，注意我们这里都没有使用激活函数，第一个神经元接收到输入层的输入，按照如下计算：
$$
z_1=w_1 \times x + b_1 = 0.1 \times 1 + 0.1 = 0.2
$$
第二个神经元接收到输入层的输入，按照如下计算:
$$
z_2=w_2 \times x + b_2 = 0.2 \times 1 + 0.2 = 0.4
$$

输出层：最后，将数据从最后一个隐藏层传递到输出层。输出层的神经元也将输入加权求和，并应用一个激活函数。输出层的输出通常是神经网络的最终预测结果。拿我们的神经网络来说，输出有一个神经元，注意我们这里都没有使用激活函数，接收隐藏层的输出作为输入，按照如下计算：

$$
z_3=w_3 \times z_1 + w_4 \times z_2 + b_3 = 0.3 \times 0.2 + 0.4 \times 0.4 + 0.3 = 0.52
$$

但要注意的是，这里只是拿一条数据来说明前向计算，实际上训练多少条数据就得计算多少条，但这个计算可以使用线性代数进行简化，有兴趣同学可以自行了解。

损失计算

当我们获取到神经网络中输出层的输出层，怎么知道其计算的对不对呢？这时我们需要使用损失函数来进行评估了，因为预计打车费用是一个线性问题，所以我们这里使用的损失函数是均方误差。如图43所示：

图43 神经网络损失计算

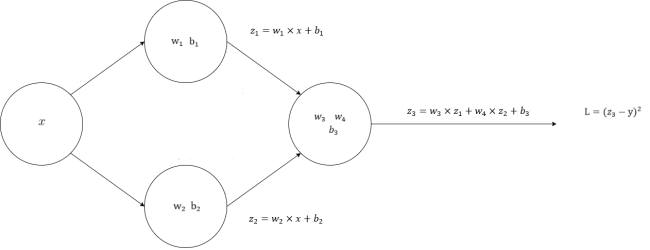
拿我们的神经网络来说，输入一条数据 [1.0, 15.0] 为例，如下计算其损失：

$$
L=(z_3-y)^2=(0.52-15.0)^2 \approx 209.67
$$

这样我们就可以通过损失值，就可以看出来神经网络的参数是否合适，损失值越大，参数越不合适；损失值越小，参数越合适。

但要注意的是，这里只是拿一条数据来说明前向计算，实际上训练多少条数据就得计算多少条，即平均计算所有数据的损失。

反向传播

所谓反向传播是从输出层开始，计算每一层的梯度，即损失函数对每个权重和偏差的偏导数。这是通过链式法则来实现的。为了不在反向链式求导的过程中临时计算某些偏导数，我们如图44所示：

图44 神经网络反向传播1

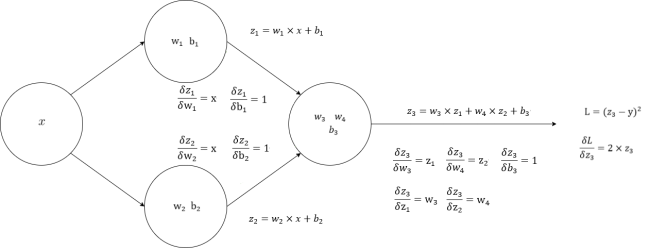
把每个神经元输出对于各个参数的偏导数都计算出来。首先是隐藏层的，计算如下：
$$
\frac{δz_1}{δw_1}=x=1,\frac{δz_1}{δb_1}=1,\frac{δz_2}{δw_2}=x=1,\frac{δz_2}{δb_2}=1
$$

其次是输出层的，计算如下：
$$
\frac{δz_3}{δw_3}=z_1=0.2,
\frac{δz_3}{δw_4}=z_2=0.4,
\frac{δz_3}{δb_3}=1,
\frac{δz_3}{δz_1}=w_3=0.3,
\frac{δz_3}{δz_2}=w_4=0.4
$$
最后神经元输出$z_3$对于损失函数针对的偏导数，计算如下：
$$
\frac{δL}{δz_3}=2 \times (z_3 - y) = 2 \times (0.52 - 0) = 1.04
$$

得到上述这些偏导数后，我们就使用求导链式法则，反向的从输出层到隐藏层分别计算各个权重和偏置对于损失函数的偏导数，如图45所示：

图45 神经网络反向传播2

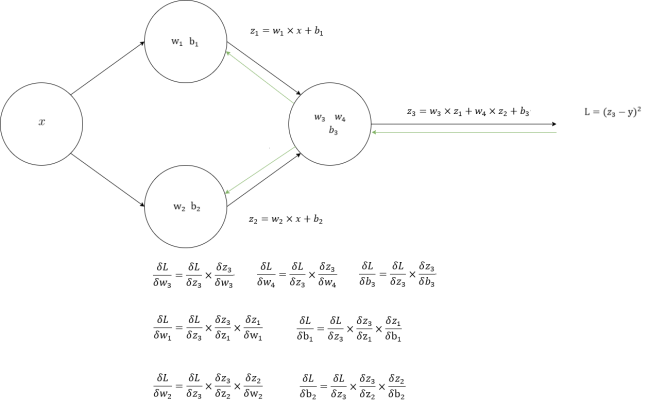
首先，输出层的偏导数，计算如下：
$$
\frac{δL}{δw_3}=\frac{δL}{δz_3} \times \frac{δz_3}{δw_3}=1.04 \times 0.2 = 0.208
$$

$$
\frac{δL}{δw_4}=\frac{δL}{δz_3} \times \frac{δz_3}{δw_4}=1.04 \times 0.4 = 0.416
$$

$$
\frac{δL}{δb_3}=\frac{δL}{δz_3} \times \frac{δz_3}{δb_3}=1.04 \times 1 = 1.04
$$

其次，隐藏层的偏导数，计算如下：

$$
\frac{δL}{δw_1}=\frac{δL}{δz_3} \times \frac{δz_3}{δz_1} \times \frac{δz_1}{δw_1}=1.04 \times 0.3 \times 1 = 0.312
$$

$$
\frac{δL}{δb_1}=\frac{δL}{δz_3} \times \frac{δz_3}{δz_1} \times \frac{δz_1}{δb_1}=1.04 \times 0.3 \times 1 = 0.312
$$

$$
\frac{δL}{δw_2}=\frac{δL}{δz_3} \times \frac{δz_3}{δz_2} \times \frac{δz_2}{δw_2}=1.04 \times 0.4 \times 1 = 0.416
$$

$$
\frac{δL}{δb_2}=\frac{δL}{δz_3} \times \frac{δz_3}{δz_2} \times \frac{δz_2}{δb_2}=1.04 \times 0.4 \times 1 = 0.416
$$

但要注意的是，这里只是拿一条数据来说明反向传播，实际上训练多少条数据就得反向计算多少次，之后再平局各个权重与偏置的梯度值，因为所有权重与偏置的调整要尽量兼顾所有的数据，这样神经网络学习到权重与偏置才能更好的拟合训练的数据。

参数更新

按照上面得到各个权重与偏置的梯度值之后，我们就可以使用梯度值，加上学习率来对参数进行更新，这里所谓参数指的就是权重与偏置，比如假设我们使用的学习率值为0.01，那么我们可以按照如下计算跟新参数：
$$
w_1=w_1 - a \times \frac{δL}{δw_1} = 0.1 - 0.01 \times 0.312 = 0.09688
$$

$$
w_2=w_2 - a \times \frac{δL}{δw_2} = 0.2 - 0.01 \times 0.416 = 0.19584
$$

$$
w_3=w_3 - a \times \frac{δL}{δw_3} = 0.3 - 0.01 \times 0.208 = 0.29792
$$

$$
w_4=w_4 - a \times \frac{δL}{δw_4} = 0.4 - 0.01 \times 0.416 = 0.39584
$$

$$
b_1=b_1 - a \times \frac{δL}{δb_1} = 0.1 - 0.01 \times 0.312 = 0.09688
$$

$$
b_2=b_2 - a \times \frac{δL}{δb_2} = 0.2 - 0.01 \times 0.416 = 0.19584
$$

$$
b_3=b_3 - a \times \frac{δL}{δb_3} = 0.3 - 0.01 \times 1.04 = 0.2896
$$

就这个参数更新计算可以使用线性代数进行简化，有兴趣同学可以自行了解。到此，我们就把神经网络的前向传播，损失计算，反向传播，参数更新给大家讲完了，但是大家要注意，这个过程不只做一次，具体执行多少次，跟神经网络的迭代次数epochs有关，假设迭代次数是10次，那么这个过程就得执行10次，依此类推。