双目测距实验

世界坐标系与相机坐标系

在进行计算机视觉任务时，通常需要将物体的位置从世界坐标系转换到相机坐标系，或者反之，以便更容易进行相机成像和图像处理操作。这些坐标系之间的转换通常涉及到矩阵变换和几何变换，例如平移、旋转和缩放等操作。通过在不同坐标系之间进行变换，可以实现物体在三维空间和二维图像之间的映射，从而进行各种计算机视觉任务，如目标检测、立体测距和三维重建等。

1.世界坐标系（World Coordinate System）：

世界坐标系是一个固定的、全局的坐标系，通常用于表示场景中的物体的真实位置和姿态。这个坐标系的原点通常位于某个参考点，例如一个地标或者场景的中心，它的坐标轴通常与现实世界中的方向相对应，例如，x轴可能指向东方，y轴指向北方，z轴指向上方。物体在世界坐标系中的位置和旋转是相对于这个全局坐标系来描述的。

2.相机坐标系（Camera Coordinate System）：

相机坐标系是相对于摄像机或相机视角而言的坐标系。它的原点通常位于摄像机的光学中心（成像平面前面的点），而坐标轴的方向通常与相机的光学系统有关。通常情况下，相机坐标系的x轴指向成像平面的右侧，y轴指向成像平面的上方，z轴指向成像平面的前方（即相机的视线方向）。物体在相机坐标系中的位置和姿态描述了它相对于摄像机的位置和朝向。

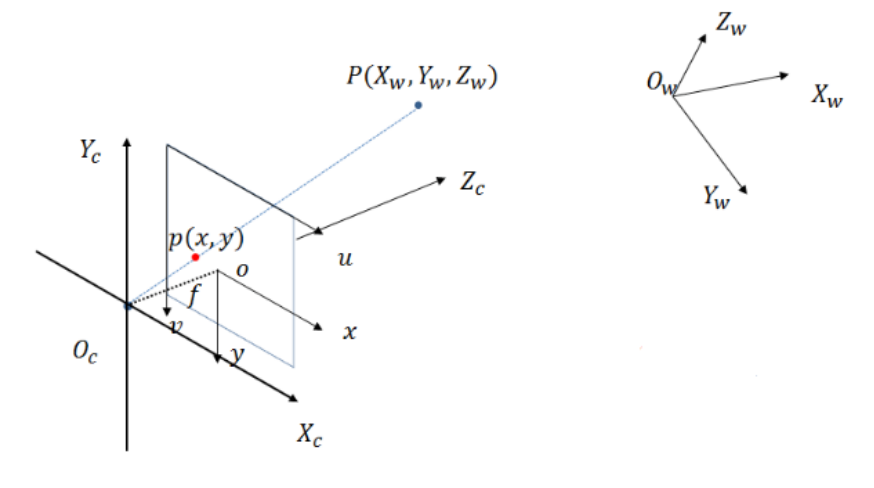
相机坐标系和世界坐标系之间的坐标转换

假设相机坐标系为 $X_cY_cZ_c$，其中 $O_c$ 为相机坐标系的原点，世界坐标系为 $X_wY_wZ_w$。我们有一个空间中的任意一点 $Q$，要完成从世界坐标系到相机坐标系的转换，可以使用以下公式：

$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=R\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+T=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\ast \left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]$

其中：

• $T$ 代表平移向量，它是相机的位置相对于世界坐标系的平移。
• $R$ 是一个三阶单位旋转矩阵，满足以下条件：
  • $r_{11}^2 + r_{21}^2 + r_{31}^2 = 1$
  • $r_{12}^2 + r_{22}^2 + r_{32}^2 = 1$
  • $r_{13}^2 + r_{23}^2 + r_{33}^2 = 1$

这个转换公式可以改写为齐次坐标形式，其中 $R$ 和 $T$ 组成了相机的外参（旋转矩阵和平移向量），它们随着相机位置和朝向的变化而变化：

$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& T\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$

这个形式适用于相机坐标系和世界坐标系之间的坐标转换，常用于计算机视觉和计算机图形学中的应用。

未完待续…..